Human Pose as Compositional Tokens
摘要
本文观察到在存在遮挡情况下的姿态检测案例中会出现被遮挡部分的不合理现象,因此引入 VQVAE 框架以尽可能在遮挡情况下获得近真实的姿态。整体思路非常简单,关键在于其 VQVAE 部分实际上是对姿态坐标 $(17,2)$ 的重建,这样少量的信息能够被真实有效重建,其中必然包含了特殊设计(姿态转化为 M 个 token)以及漫长的调试。
概览

创新
- 一种专门针对姿态检测的 VQVAE 编码器
- 使用 M 个解耦向量对姿态进行表述,每个向量有属于的对应类别,从此类别估计关键点
tricks
- 使用 ema 更新 codebook,而非梯度更新
- 使用 MAE 的方式进行训练
- 不使用 index 计算 CE,而是使用对应的 logit
- 使用 soft 的方式计算 VQ
- 在第二阶段不训练编码器,锁住解码器和 codebook,将 backbone 内嵌编码器
网络
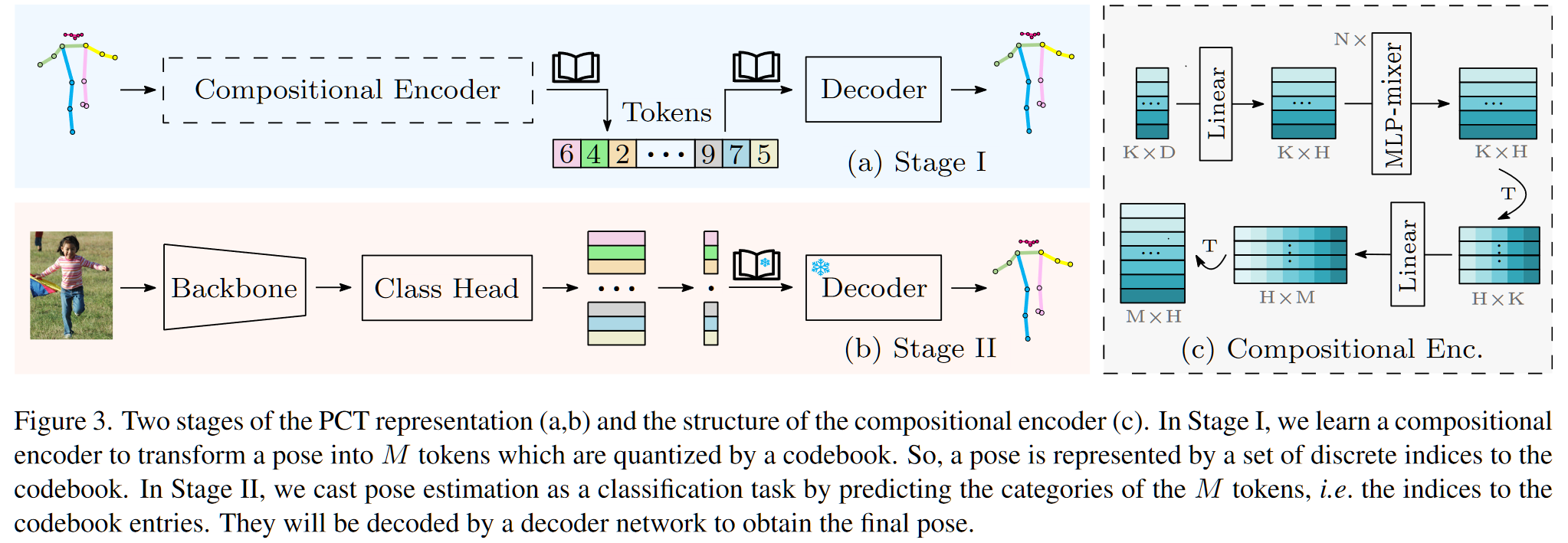
整体来说,整个前向过程比较 naive,使其有效的过程在我看来有两个关键:1.对于 VQ 的训练,编码器采用适度复杂的扩张网络,解码器和编码器对应,并且给 latent code 一定的含义;2.第二阶段相比于其他的 VQVAE 难训练得多,因为这里二阶段剔除了编码器,而是使用一个结构类似的“四层 MLP-Mixer”进行训练,这里是从零训练,会不会太难?是否可以考虑使用 label 进行深度监督?
其前向过程表示为:
stage-1
- 将原始姿态数据表示为 $G\to(K,D)$,其中 $K$ 表示有多少关键点,本文选择 $K=17$,$D$ 表示每个关键点的位置表征,在 2D 的情况下,$D=2$
- 将 $G$ 输入编码器 $f_e$,得到一个包含 M 个向量的集合 $T=\{t_i\}_i^M$
- 对 $T$ 进行 VQ,VQ 过程使用 NN 方法,从而得到使用 codebook $C=(c_1,\dots,c_V)^T\to(V,N)$ 的表示:$\hat T=\{c_{q(t_i)}\}_i^M$
- 将 $\hat T$ 输入解码器 $f_d$,得到重建姿态 $\hat G$
- 计算 loss:$L_{pct}=L_1(G,\hat G)+\beta\sum\limits_{i=1}^M||t_i-sg[c_{q(t_i)}]||_2^2$
- codebook 更新问题:这里只有对 codebook 的梯度裁剪,也就是说对于 codebook 没有采用梯度更新,文中阐述采用 ema 进行更新(V100:/root/code/PCT/models/pct_tokenizer.py:155)
stage-2
- 原始输入图像为 $I$,使用对应的 backbone 提取特征为 $X$,$X$ 的 shape 不重要,因为接下来会使用一些 proj 改到固定 shape
- 将 $X$ 经过一个特征调制器 $\cal C$ 和一个线性投影头 $\cal L$ 之后得到:$X_f=\mathcal L(\mathrm{Flatten}(\mathcal C(X)))\to(M,N)$
- 此时,$X_f$ 已经和 $T$ 的 shape 一致,但是为了保证具备 stage-1 编码器能力,额外加入一些 MLP
- 由四层 MLP-Mixer(近似 stage-1 Encoder)进行编码,得到 $\hat L=\mathcal M(X_f)\to(M,V)$
- $\hat L$ 的每一行的 $V$ 列表示 $V$ 个 codebook index 的预测概率
- 由此计算和 GT 的 CEloss $L_{cls}=CE(\hat L,L)$
- 这里的 $L$ 来自于真正的 $G$ 在 stage-1 中的 VQ 结果,其 shape 为 $(M,1)$,由于来源于 NN,只包含最终的类别,计算 CE 时进行广播
- stage-2 中计算的 $\hat G=f_d(S)$,其中 $S=\hat L\times C$,$C$ 就是 codebook
- 计算重建损失 $L_1(\hat G,G)$,因此 stage-2 的 loss 最终为:$L=CE(\hat L,L)+L_1(\hat G,G)$
结果
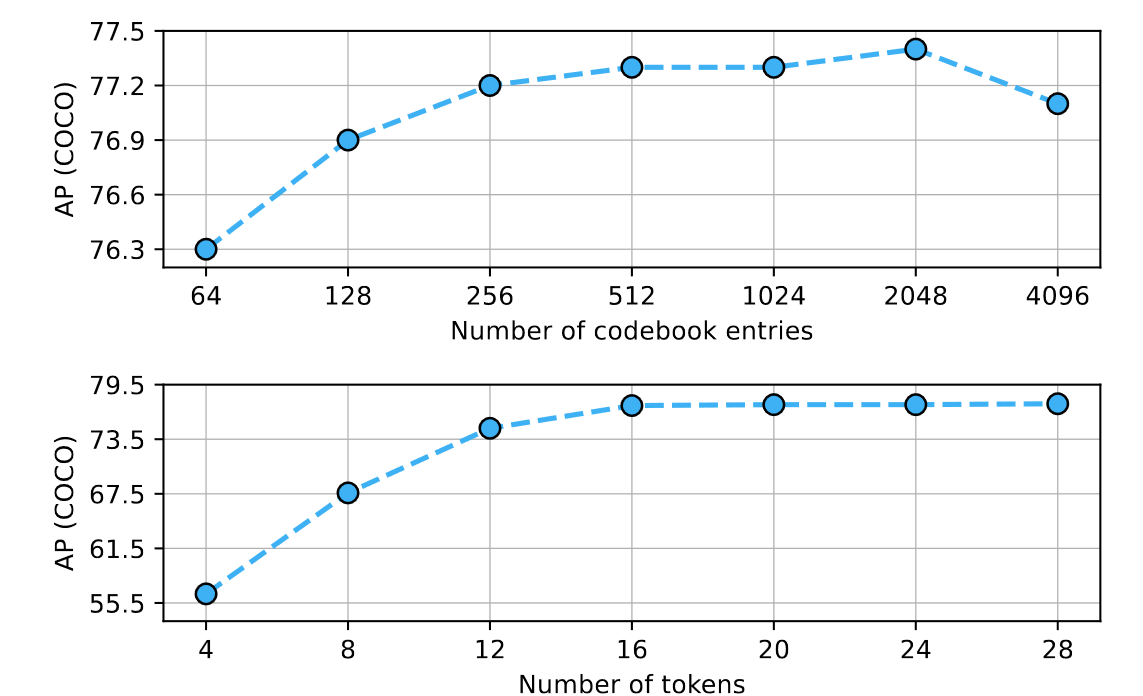
- 关于 codebook size 和 M 的选择消融实验
- 可视化效果(绿框中是遮挡也测出来的,红框中是遮挡没测出来的)
