LeetCode-11. 盛最多水的容器

LeetCode-11. 盛最多水的容器【M】

题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

1
2
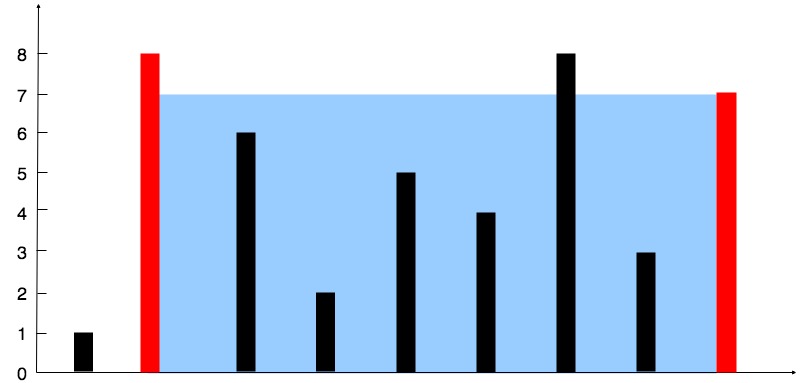
3

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

1 2	输入：height = [1,1] 输出：1

提示：

1
2
3

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

解题思路

思路

双指针法

设置两个指针 p , v 分别从头部和尾部向中间缩小，缩小策略为：①移动当前较小的指针，②当能使最大值更新的时候更新最大值。代码执行逻辑如下：

初始化最大值为两端为边的值
当左指针小于右指针时
- 向中间移动更小的那个指针
- 如果可以更新最大值则更新最大值
返回最大值

证明

这里需要证明的关键在于：在小的指针固定时，大的指针无论如何向中间移动都不可能得到更小的结果。

即：记求值函数为 $f(p,v)$ 指针 $x$ 对应的高度为 $h(x)$，若 $h(p)\leq h(v)$，则对 $\forall v’\leq v,f(p,v’)\leq f(p,v)$。这个定理的正确性保证了只移动值更小的指针就可以遍历所有可能的情况，从而得到最优解。

接下来证明该定理：

由于 $h(p)\leq h(v)$，则 $f(p,v)=(v-p)\times h(p)$，对于 $p,v’$，有 $f(p,v’)=(v’-p)\times \min(h(p),h(v’))$
由于 $v’-p\leq v-p$，且 $\min(h(p),h(v’))\leq h(p)$
从而 $f(p,v’)=(v’-p)\times \min(h(p),h(v’))\leq (v-p)\times h(p)=f(p,v)$
即得证

该方法时间复杂度为 $O(n)$，空间复杂度为 $O(1)$

代码

class Solution:
    def maxArea(self, height: List[int]) -> int:
        p,v = 0,len(height)-1
        maxs = (v-p)*min(height[p], height[v])
        while p<v:
            if height[p] <= height[v]:
                nmax = (v-p-1)*min(height[p+1], height[v])
                if nmax > maxs:
                    maxs = nmax
                p += 1

            else:
                nmax = (v-p-1)*min(height[p], height[v-1])
                if nmax > maxs:
                    maxs = nmax
                v -= 1
           
        return maxs