SiNC

Non-Contrastive Unsupervised Learning of Physiological Signals from Video

【rPPG】【CVPR2023】【paper】【code】

abstract

  本文基于 PPG 信号的三个特征，提出了一种非对比学习的自监督方法用于 rPPG 测量，虽然作者强调了没有针对 rPPG 进行独特的网络设计，但是三种特征均为 PPG 信号强相关的，并且这项工作实际上可以看做“基于负样本和先验约束的对比学习”。需要指出：作者认为在同 batch 内的 PSD 之和应当分布均匀，这是显然不成立的，即使考虑 batch size 可以很大并且视频经过数据增强，在统计学意义上 PSD 之和仍应该服从正态分布。

overview

---

contribution

• “非对比学习”的无监督结构（事实上可以看做是对比学习的变体）
• 三个针对“频率任务”进行优化的损失函数：sparsely，bandlimits，variance

formulation

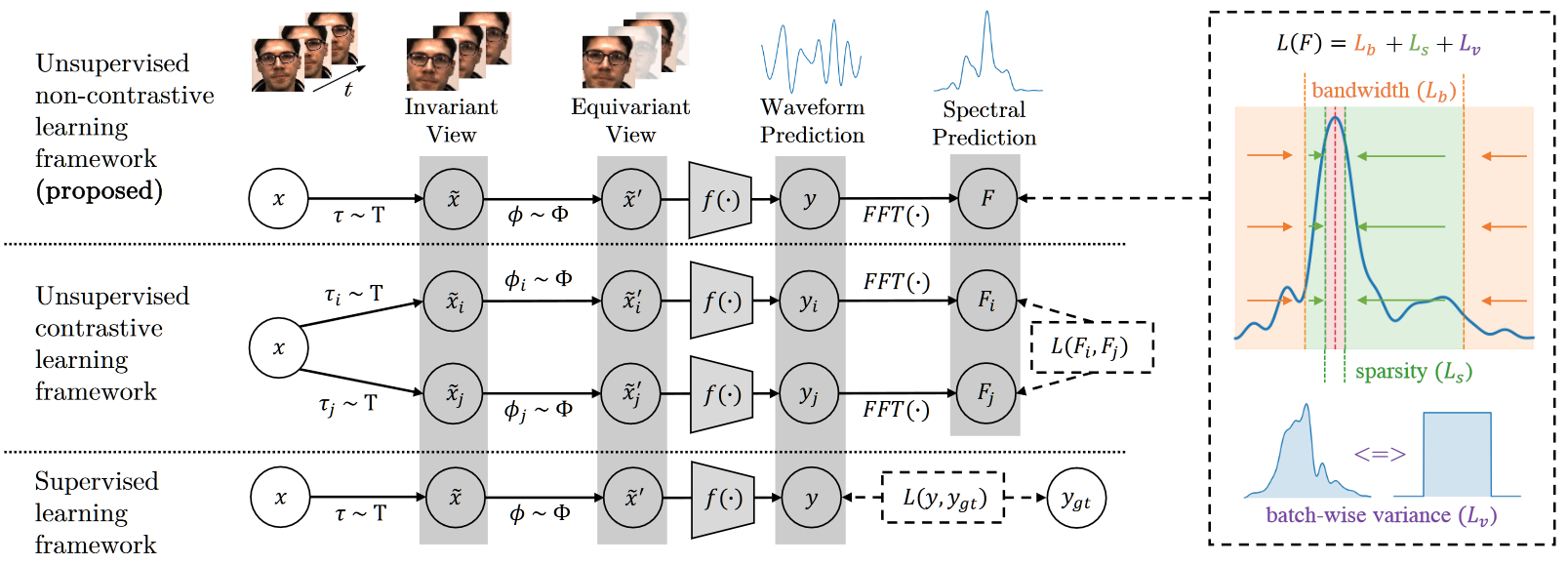
  输入 video $x_i\in\mathbb{R}^{T\times W\times H\times C}$；数据增强的操作集合 $\Phi$；来自 SOTA（physnet）的模型 $f$；波形 $y_i=f(x_i)$；波形频率 PSD $F=\mathrm{FFT}(y)$；$F_i$ 表示 $F$ 在频率为 $i$ 的分量；正常人的 PPG 信号频率在 $a=0.66\mathrm{Hz}\rightarrow b=3\mathrm{Hz}$ 之间变化。

framework

  本文的关键不在于网络而是损失函数的设计，在模型上选取了简单的 physnet。

• Sparsity Loss：此损失防止频率的带宽过分散

$$L_s=\frac{\sum\limits_{i=a}^{\arg max(F)-\Delta F}F_i+\sum\limits_{i=\arg max(F)+\Delta F}^{b}F_i}{\sum\limits_{i=a}^{b}F_i}$$

  其中，$\arg max(F)$ 即为心率，而 $\Delta F$ 表示 $\pm0.1\mathrm{Hz}$ 范围内的频率。也就是说，这个损失函数的意义为：在 $\arg max(F)\pm0.1\mathrm{Hz}$ 之外的频率图面积和总频率图面积之比，优化方向为：使 PSD 更集中在 $0.1\mathrm{Hz}$ 之内。

• Bandwidth Loss：此损失防止带宽离开心率频率范围之外

$$L_b=\frac{\sum\limits_{i=-\infty}^{a}F_i+\sum\limits_{i=b}^{\infty}F_i}{\sum\limits_{i=-\infty}^{\infty}F_i}$$

  这个损失函数的意义为：小于 $a$ 或大于 $b$ 的频率图面积和所有可能的频率面积之比。优化方向为：使 PSD 集中在 $[a,b]$ 之内（事实上就是 IPR 越小越好）

• Variance Loss：此损失防止模型 collapse

  在只有前面两个损失函数的情况下，仅仅能限制模型输出“正确”的信号而非“对应”的信号，本文通过将同一个 batch 内输出的 PSD 方差增大期望模型学到正确信号。

$$L_v=\frac1d\sum\limits_{i=1}^{d}(\mathrm{CDF}_i(Q)-\mathrm{CDF}_i(P))^2$$

  其中 CDF 是累计分布函数，$\mathrm{CDF}_i$ 就表示 Q 分布在第 i 个频率的分量，这里 Q 和 P 都是 (1, d=140) 的 tensor。可以这样理解：Q 表示对一个 batch 内所有的 PSD 直接求和的结果，而 P 则是单纯的均匀分布。使 Q 靠近 P 即为：在同一个 batch 内，PSD 的峰值应当分散一些，从而让整个 batch 的 PSD 求和等于均匀分布。

experiment

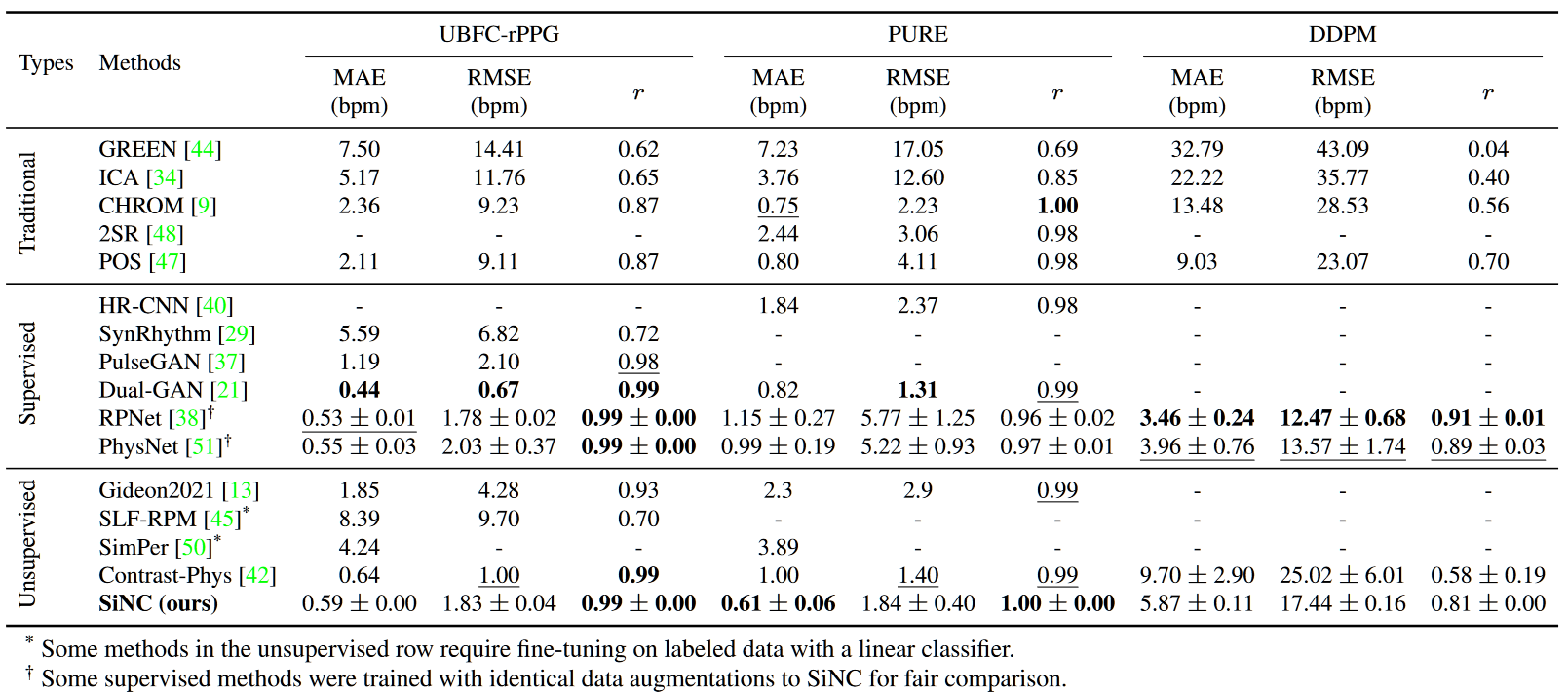
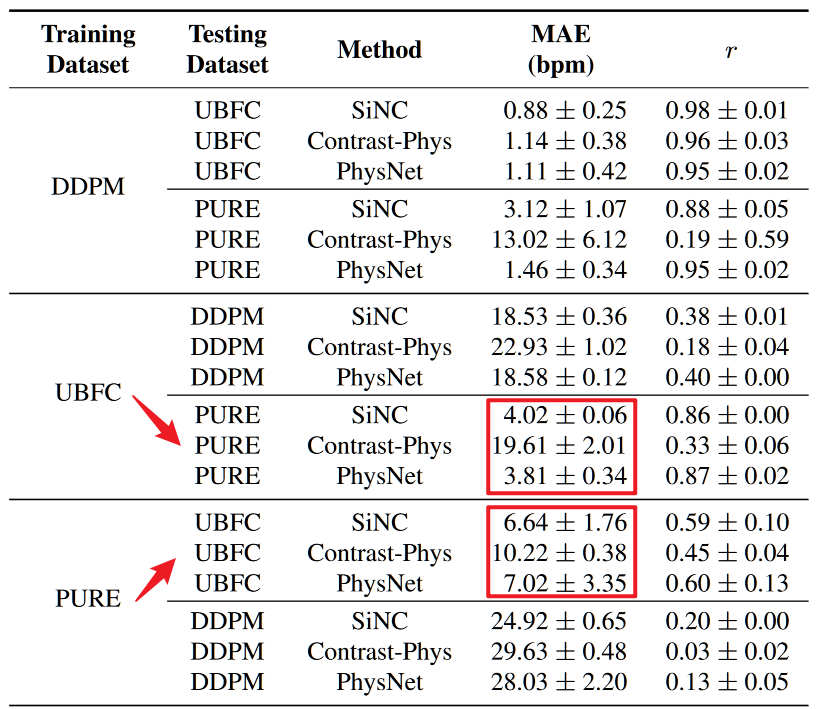
  intra- 中规中矩，cross- 效果比较差，但是本文列出的其他 SOTA 实验结果也差，也就是说实际上本文重新跑了其他 SOTA 的跨数据集。