Self-similarity Prior Distillation for Unsupervised Remote Physiological Measurement
abstract
本文提出了一种新的 rPPG 自监督结构,相对于对比学习强调的正负样本,本文更关注 rPPG 信号的自相似性,这种自相似性可以看做周期性,所谓的“分层蒸馏”也是正样本对的一种形式。尽管对比学习本身没有明确的缺点,但有些文章喜欢通过和对比学习划清界限显得自己很 novel。事实上本文也用到了正样本对,并且由于没有负样本的有效性监督,需要指出本文提出的 SSPD 结构在逻辑上无法避免模型的模式崩溃。
overview
contribution
- 一个基于自相似性挖掘和知识蒸馏的无监督框架 SSPD
- 一种自相似性(周期性)的度量方法
framework
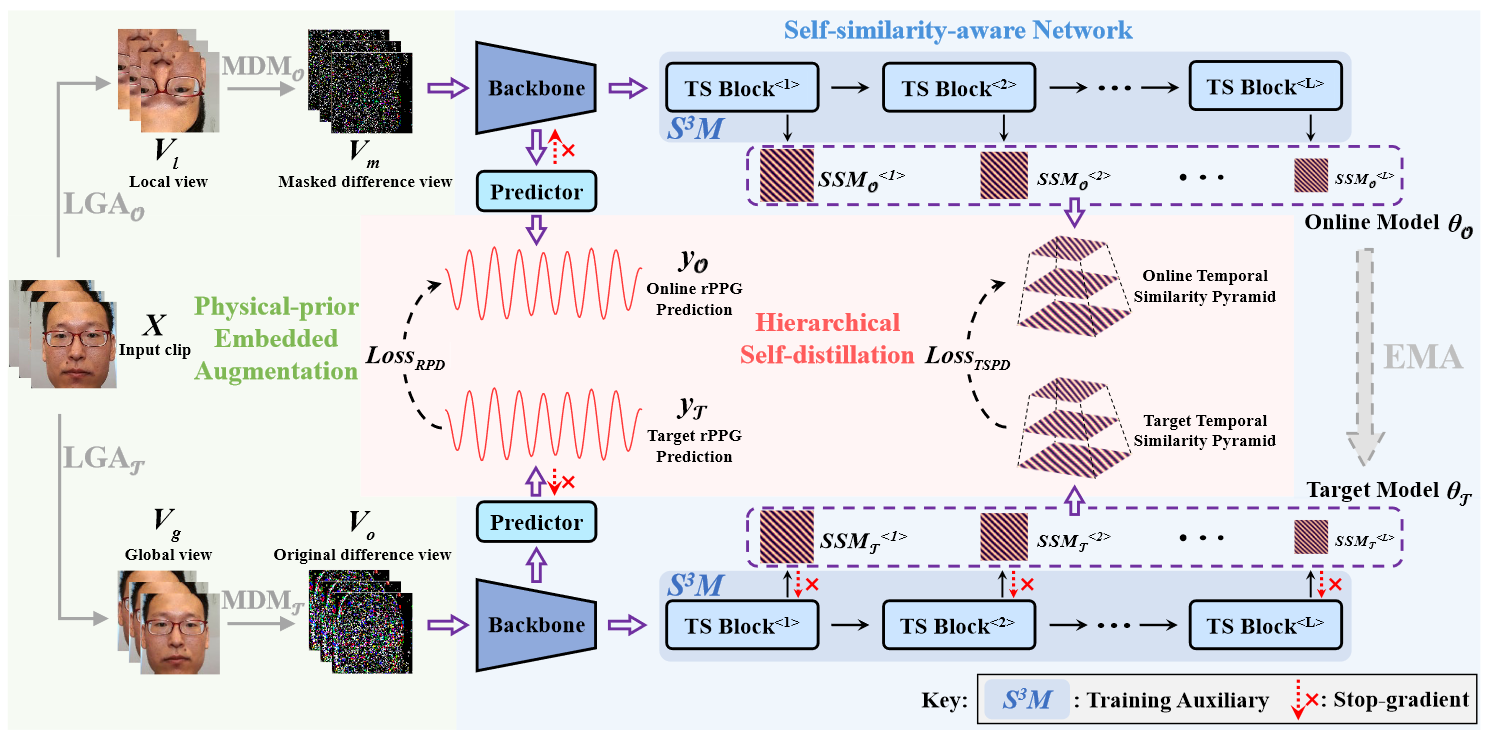
由于整个模型架构是蒸馏的体系,因此所有的损失函数都不更新 target 部分,而是通过更新 online 部分之后再 EMA 同步到 target 分支。
- 对于 input clip $X$,其分别在 online 分支和 target 分支进行数据增强得到 $V_m,\ V_o$
- $V_m=M\odot\Delta V_l,\ V_l=\mathrm{Crop \& Flip}(X)$,其中 $M=\{m_i\}_{i=1}^T,\ m_i\in\{0,1\}$,对每一帧随机采样。也就是裁剪、翻转、差分、随机 mask
- $V_0=\Delta V_g,\ V_g=\mathrm{Flip}(X)$,也就是翻转、差分
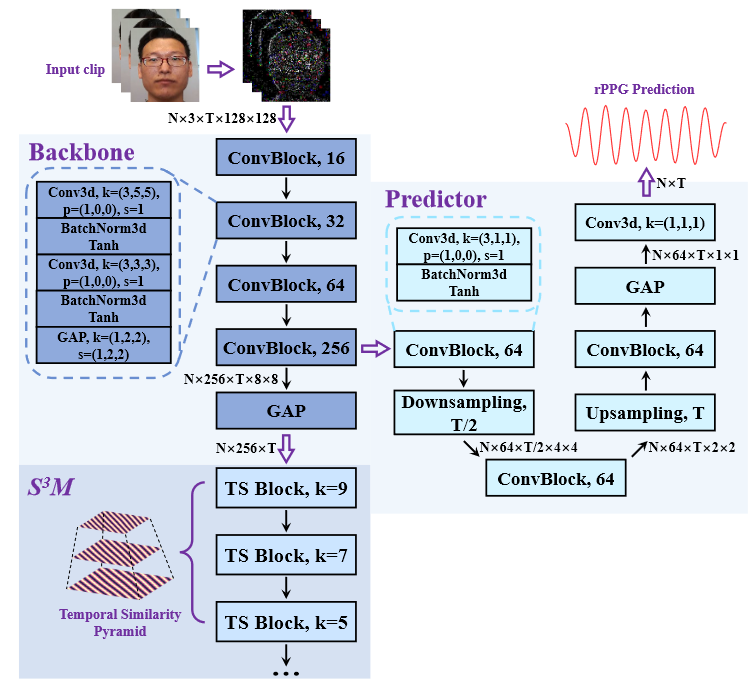
- 将 $V_m,\ V_o$ 分别输入两个 backbone,在 backbone 的最后一层和倒数第二层分别返回 $F_1\to(N,256,T),\ F_2\to(N,256,T,8,8)$,这两个 feature 将分别用于蒸馏和 rPPG 预测
- 对于 rPPG 预测部分,online 分支输出 $y_o$,target 分支输出 $y_t$
- 对于 $y_o$ 和 $y_t$,计算 NP 和 MSE of PSD:$\mathcal{L}_{RPD}=\mathrm{NP}(y_o,y_t)+\mathrm{MSE}(\mathrm{PSD}(y_o),\mathrm{PSD}(y_t))$
- 需要特别指出,这里的损失不更新 backbone,只更新 online 分支的 predictor(文章说避免梯度冲突,我觉得有点扯。。。)
- 对于蒸馏部分,online 和 target 分支分别通过 $L$ 个 TS Block,每个 Block 输出一个独特 scale 的自相似图 $\mathrm{SSM}$,多个不同 scale 的 $\mathrm{SSM}$ 组成自相似图集合
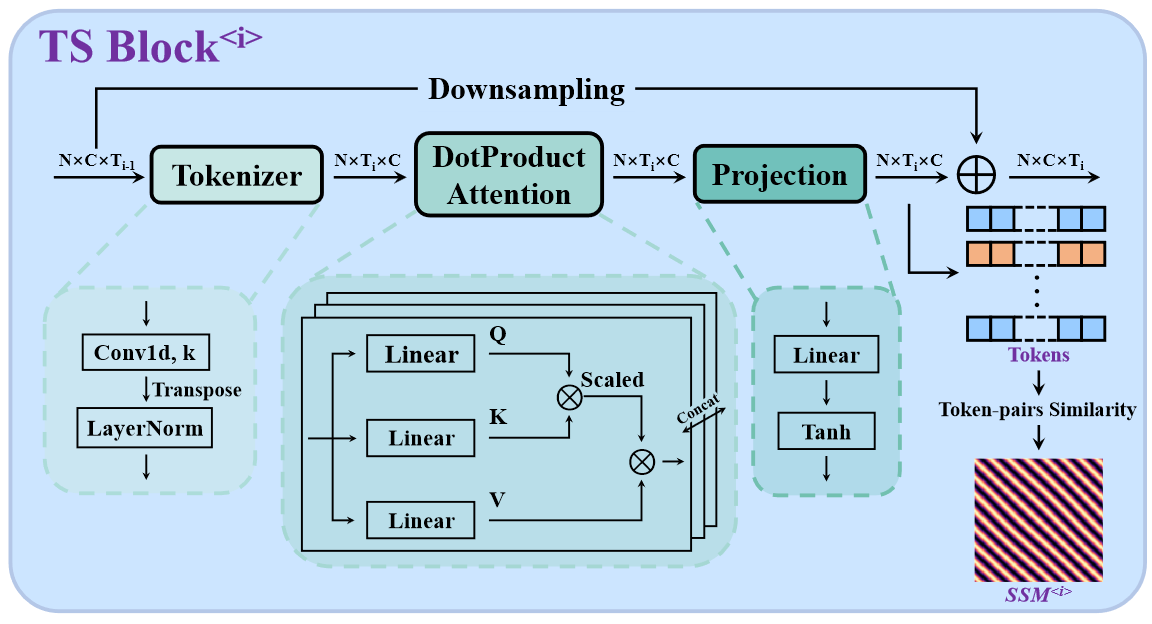
- 对于每个 TS Block,输入为 $S\to(T_{i-1},C)$,$T_{i-1}$ 表示第 i 个 TS Block 输入的时间维度
- 首先将 $S$ 进行 embedding(同时降采样)到 $E\to(T_i,C)$
- 接着计算 transformer 前向,$A=\frac{QK^T}{C}\cdot V\cdot W\to(T_i,C)$,其中 $W\to(C,C)$ 是 proj,每个 TS Block 的输出是 $E+A$
- 使用 $A$ 计算相似性图:$\mathrm{SSM}=\{\mathrm{CosSim}(A_j,A_k)|j,k\in[1,T_i]\}\to(T_i,T_i)$
- 使用相似性图计算相似性波 SSW,计算方法为将 SSM 上三角沿着的对角线重排,得到 $D=\{d_i\}_{i=1}^{T_i}$(注意不同的 $d_i$ 长度也不同),对 $D$ 计算均值即可得到 $\mathrm{SSW}\to(T_i,1)$
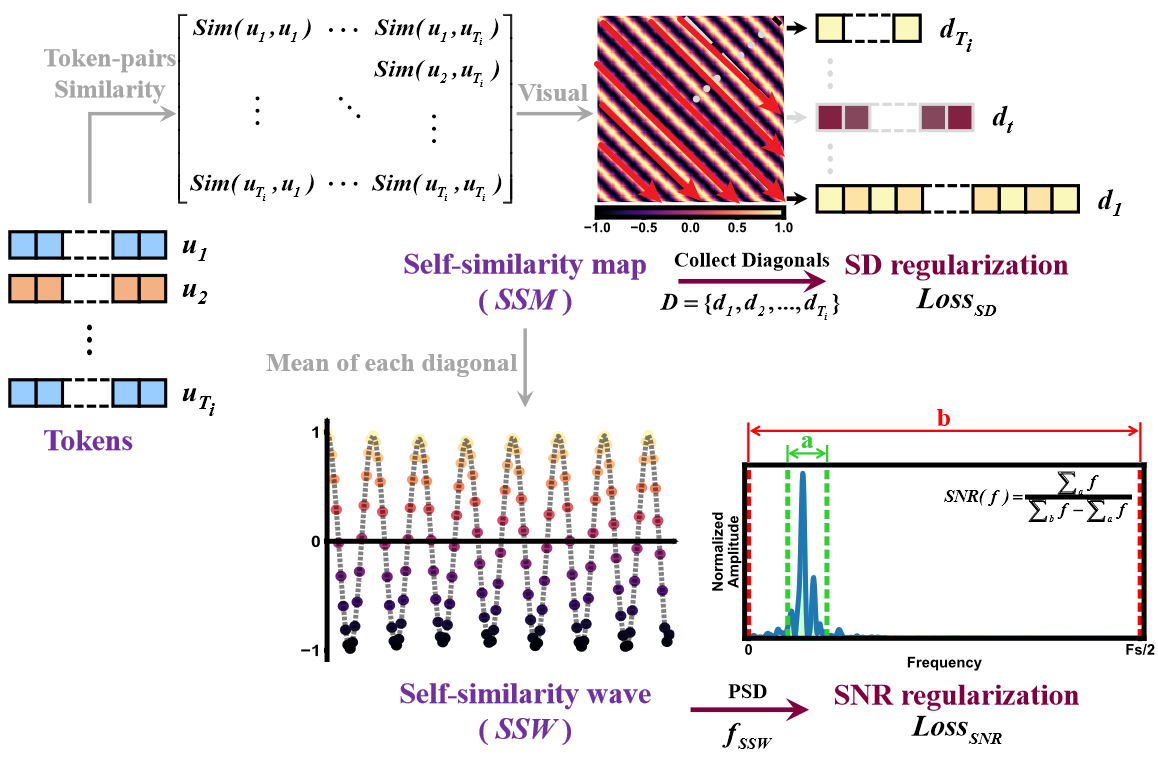
- 对于 online 和 target 分别得到的自相似性图集合 $\mathcal{SSM_O,\ SSM_T}$ 和自相似性波集合 $\mathcal{SSW_O,\ SSW_T}$ 计算蒸馏损失:
- $\mathcal{L}_{MSE}=\mathrm{MSE}(\mathcal{SSM_O,\ SSM_T}) + \mathrm{MSE}(\mathcal{SSW_O,\ SSW_T})$
- $\mathcal{L}_{TSPD}=\mathcal{L}_{MSE}+\alpha\mathcal{L}_{SD}(\mathcal{SSM_O})+\beta\mathcal{L}_{SNR}(\mathcal{SSM_O}),\ \mathrm{where\ \alpha=0.04,\ \beta=0.6}$
- 需要指出,虽然文章里 $\alpha=0.8$,作者这里玩了个 trick,因为 SD 损失里面还有个 0.05 的系数,这实际上意味着 SD 也许用处不大,甚至可能降点
- 其中 SD 损失就是 $D$ 里面的每个 $d_i$ 的标准差的均值;SNR 就是 PSD 中在 [0.5, 3Hz] 的面积和 [0, 15Hz] 的面积之比 ,SNR 损失是 $\mathcal{SSW_O}$ 中所有波形的 1/SNR 之和。
总体来说,SSPD 的损失定义为:$\mathcal{L}_{SSPD}=\mathcal{L}_{RPD}+\mathcal{L}_{TSPD}$,$\mathcal{L}_{RPD}$ 只更新 online 分支的 predictpr,$\mathcal{L}_{TSPD}$ 更新 online 分支的其他。target 分支由 EMA 更新。

必须指出,在现在的损失函数下,模型存在寻找捷径的可能,模型可以通过无论什么输入都输出相同的 rPPG 信号让损失降到最低。无论实验结果如何,模型的模式崩溃并没有在设计上得到解决。
experiment
rPPG community dddd