Exploration into Translation-Equivariant Image Quantization
【VQGAN探索】【ICASSP(CCF_B)】【paper】【code未开源】
摘要
本文提出了在 VQ 的时候由于码本中不同编码的堆叠,可能导致性能的下降以及平移等变性的缺失,因此以一种很简单的方式消除了堆叠,具体来说,即加入正交化损失,通过强制 codebook 正交化减少堆叠。
概览
创新
- 正交化损失,用于减少堆叠以及保持平移等变性
- 正交初始化,用于减少堆叠(以本文为经验可以得出的结果,具备明显的合理性)
为什么要正交?
图像经过 CNN 之后的平移等变性缺失是老生常谈的话题,以可视化的例子如下所示,下图中随着图像主体的平移,普通的 CNN 结构(baseline)的置信度变化方差很大,而抗堆叠的方法会好很多。

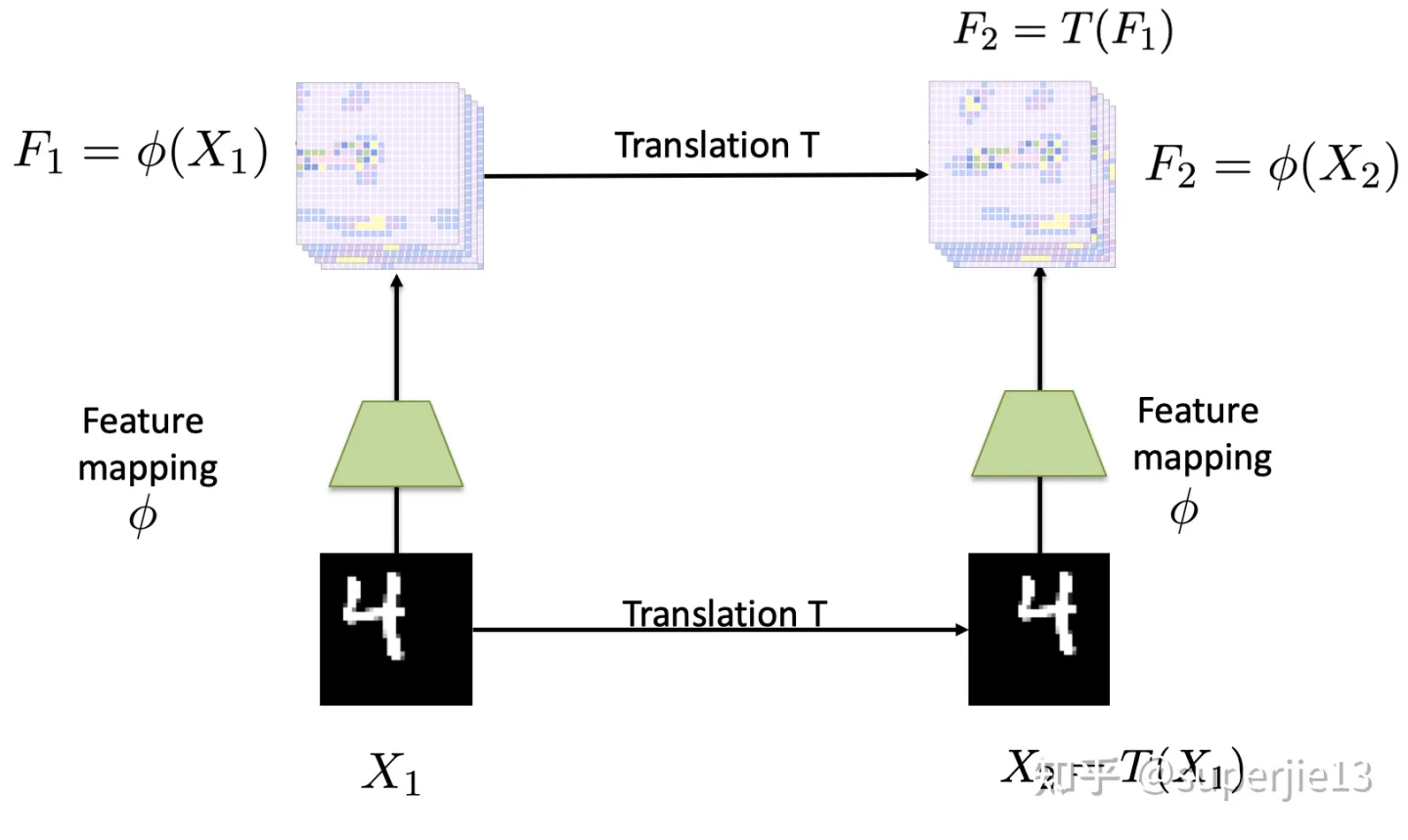
所谓平移等变,事实上在分类任务中要求的应该是平移不变性,就是平移之后输出不变,对应在分割等任务上应该是平移等变,就是平移之后输出的 box 等跟随平移。但是我觉得在分类任务其实也得要求平移等变,并非以结果和输入等变,而是以特征图和输入等变,如下图所示。而平移不变性则是在等变的特征图的基础上后续预测网络的要求。
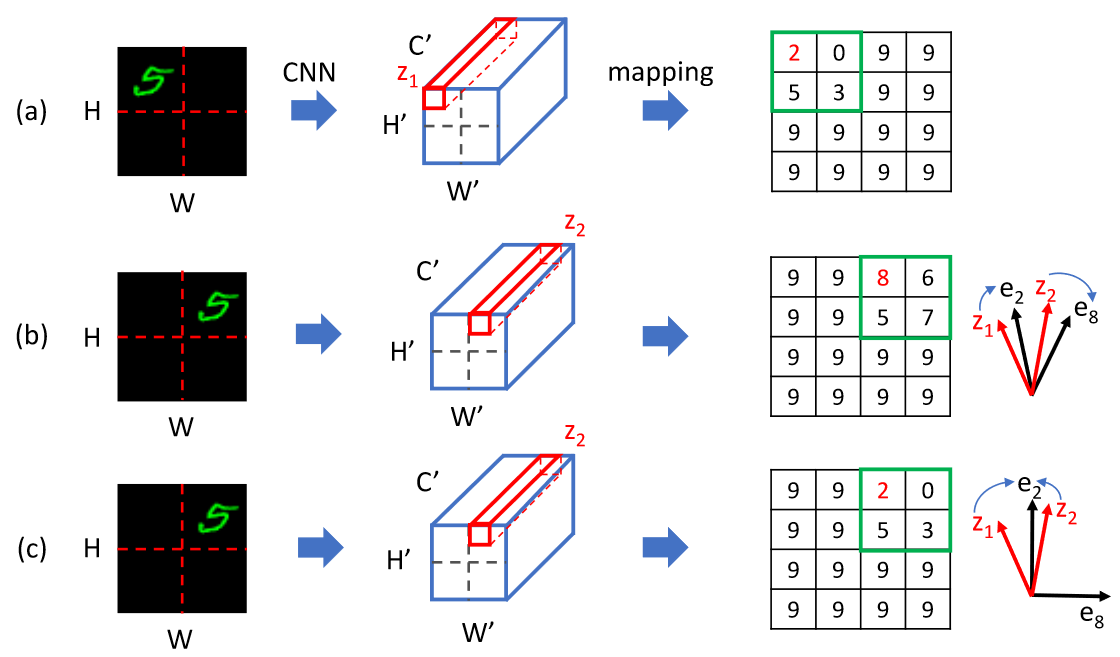
之所以会缺失平移等变性,主要是因为在降采样的过程中,无论是卷积降采样还是池化降采样,都会损失相对位置信息,以 MaxPooling 为例,第一步取 max 实际上只是在一定程度上做了平均,算是一种信息的压缩,但是这里的压缩损失的只是细节信息,但是第二步的池化操作会把原本离得或近或远的 max 的 index 放在相邻位置。这种降采样导致在周期性平移(平移长度为步长整数倍)时可以获得平移等变的结果,而除此之外就会产生较大的误差。因此可以看出 baseline 并不是一直都差,而是周期性地好坏。
如何保证码本正交?
码本的正交可以最大限度地消除码本的冗余性,从而在特征向量少量移动时保证量化之后的向量尽可能不变。
至于做法包含两个层面:
- 初始化的时候将随机初始化的变量进行正交化处理
- 使用正交化损失进行强制 codebook 正交化,orthogonality loss 写作:
即,对码表的编码进行 l2_normlize 之后计算正交矩阵,使其和单位矩阵尽可能接近,$K^2$ 用以消除尺度误差,$\lambda$ 用以平衡权重。