Meta-rPPG: Remote Heart Rate Estimation Using a Transductive Meta-Learner
摘要
本文采用了元学习的方式探索了在跨数据集上的适应性问题,通过将每个 clip 的预测看做单个任务的方式构造多任务,并将每个 clip 区分为互不相交的 Q, S 进行 few-shot 学习。得到的网络结构理论上可以在预训练的基础上支持 zero-shot 学习,通过梯度合成生成器快速学习无标签数据。缝合元学习的基础上在 MAHNOB-HCI 取得了 SOTA,在 UBFC 上效果普通。
概览
前置知识
元学习概念
元学习、自监督学习、对比学习、FSL
- 自监督学习的常用方法包括对比学习
- few-shot learning(小样本学习)是自监督学习的下游任务之一
- FSL 目的是通过不足以训练网络的样本量进行学习和预测
- FSL 通常使用迁移学习完成
- 迁移学习着眼于:1.利用先验知识快速学习新的数据集,2.在学习新数据集的基础上不忘记旧数据集
- 元学习是迁移学习的一种
元学习的含义
元学习原本的含义为 “learn to learn”,即通过学习超参数从而生产网络(有点像 NAS)
但是在本文中并没有学习超参数
事实上在当前一些带有 “Meta” 的论文其中的本质是对比学习
元学习着眼于:在同分布的任务上通过先验网络快速学习新数据集
- 获取灵活的先验网络的方式:在多个任务上进行训练
元学习最常用的任务为分类任务,其最初架构的提出与改进都在分类任务上进行测试
- 但是在本文中的任务为回归任务(创新点之一,但创新得很牵强)
- 由于常在 few-shot 任务上学习,元学习的网络结构通常不深,为了避免过拟合
元学习中的定义
- $\mathcal {Q, S}$:Query,Support,即为了区别于元学习架构中真正的测试集、训练集,重新命名在迁移的单任务中的测试集(Query Set)、训练集(Support Set)。
- N-ways,K-shot:N-在 $\mathcal S$ 中的类别数目,K-在 $\mathcal S$ 中每个类别的样本数目
一个元学习的实例
对于图像分类任务,有网络 $f_\theta$,输入图像 $x$,训练数据集 $\mathcal T$。其中训练集如下图所示:

由于元学习需要在多任务上进行训练,一个简单的想法就是把 $\cal T$ 分成多个任务,多次训练之后可以得到初始化的 $f_\theta$,输入图像 $x$ 之后可以输出在多个类别上的概率分布。
此时给出在某个小任务(训练集分出来的或者新遇到的),对于此任务,其训练集(Support Set)和测试集(Query Set)都很小,一个可能的例子如下图所示,在此任务中,由于总共有 6 个类别,每个类别只有一个样本,因此称之为 6-ways,1-shot 任务。

以训练好的 $f_\theta$ 作为初始化网络开始学习新的小数据,可以在很快的时间内学会此分类任务。
创新
- 一种可以用于心率监测的元学习框架
- 使用合成梯度生成器和分布最小化损失快速学习无标签数据
网络

网络组成
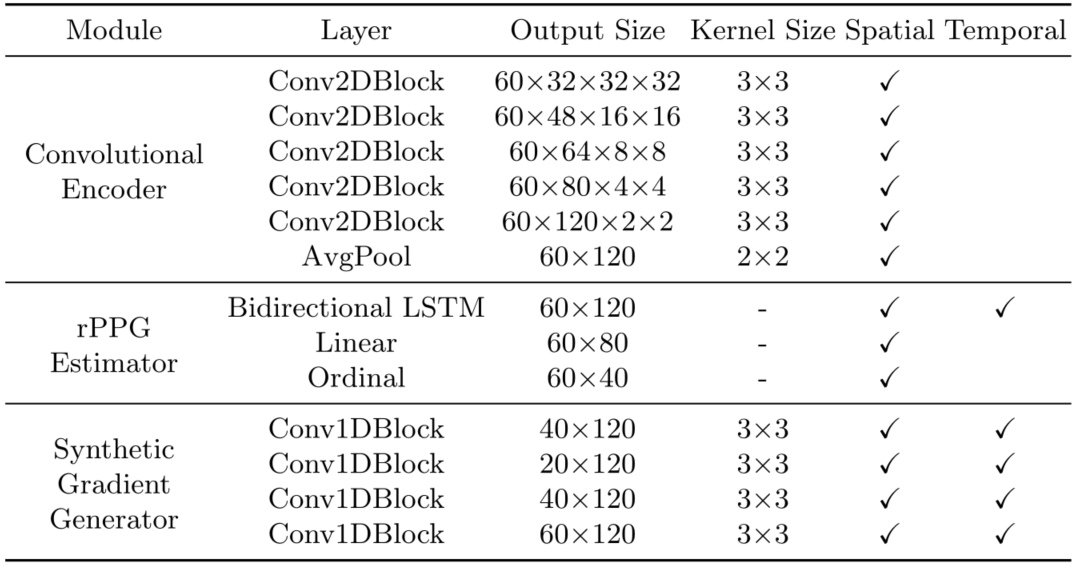
整个网络分为三个部分:特征提取器、rPPG 估计器、合成梯度生成器。前两部分首先训练,就是普通的 rPPG 估计器训练方式,分别由 Conv 和 LSTM 组成。合成梯度生成器由 Conv 组成,仅在直推学习期间使用。三个组成部分的具体网络组成如下图所示,其中 Conv2DBlocks 由Conv2D、Batchnorm、average pooling 和 ReLU 组成。Conv1D 模块由 Conv1 d、Batchnorm 和 ReLU 组成。
前向过程
对于输入 $\cal T$,首先的预处理是标定其 landmark,切割出人脸部分(这里使用的是 dlib,肯定耗时很长,又不能叫端到端啦 😅)结果记为 $x^{train}$,从训练集中取出 N 个独立的 clip,这些 clip 每一个的 ppg 信号估计都代表了一个任务。接着对每一个子任务,将 clip 分为 $V,\ W$ 帧的子 clip,分别记为 $\cal {S,\ Q}$。这样就完成了元学习的基本设定。
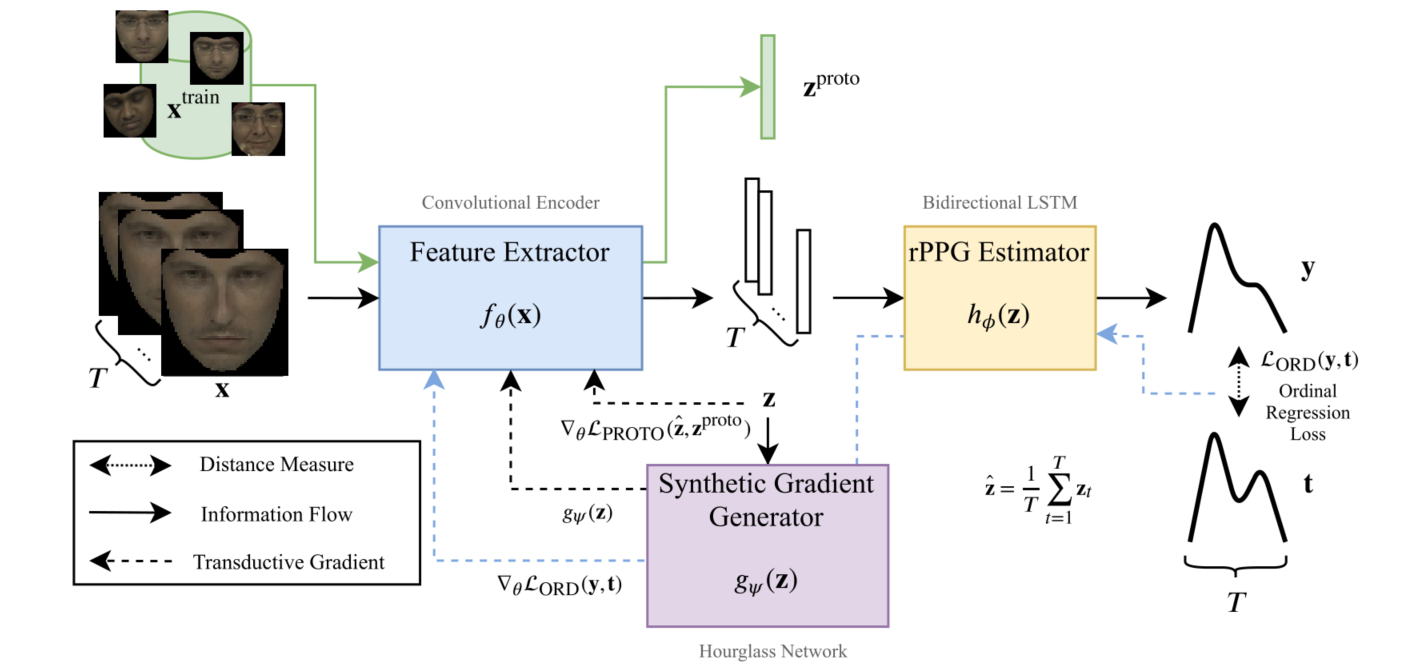
在预训练阶段,对 $x^{train}$ 采样 T 个连续帧 $x$,将其输入特征提取器,得到 $f_\theta(x)$,其中 $\theta$ 是 $f$ 的参数。这里的 $f_\theta(x)$ 是一个具有 T 长度的 ppg 信号,记为 $z$。对于 $z$,将其输入 rPPG 估计器得到 $y=h_\phi(z)$,将预测的 ppg 信号 $y$ 和 $t(y_{GT})$ 进行比较,计算 $\mathcal L_{ORD}(y,t)$后梯度回传,是一个普通的训练过程。
在直推式学习阶段,需要限制两个新的学习:1.梯度生成器的输出应当和 $\mathcal L_{ORD}$ 回传给 $z$ 的梯度一致,以便接下来的迁移学习,2.通过 $x\in\cal S$ 特征提取器生产的特征值 $z$ 应当和 $x^{train}$ 生产的 $z^{proto}$ 具备一致的分布,这是因为之前的研究已经证明:必须在同分布的数据中元学习的方式才更有效。
因此在直推式学习阶段生成 $z$ 之后,$z$ 有两个去向,除了输入进入 $h_\phi$,还会进入 $g_\psi$,对于 $g_\psi(z)$,其期望的输出应当和 $\nabla_z\mathcal L_{ORD}(y,t)$ 一致,为了限制这种一致性,计算 $\mathcal L_{SYN}=||g_\psi(z)-\nabla_z\mathcal L_{ORD}(y,t)||_2^2$,同时在直推式学习之中更新 $\theta$ 的梯度,即 $g$ 也负责将 $\mathcal L_{ORD}$ 的梯度传给 $f$。通过这种方式就限制了合成梯度生成器的学习,而在之后的无标签学习中,就可以通过 $g$ 生成的梯度来辅助更新 $f$。
同时为了保证 $\cal S$ 生成特征的分布一致性,记 $\hat z = \frac 1 T \sum\limits_{t=1}^Tz_t$,为了在统计 $z^{proto}$ 在整个数据集上的分布特性,通过迭代的方式随着预训练统计,其具体更新公式为:
因此计算分布一致性损失 $\mathcal L_{PROTO}=\mathbb E_{x^{(i)}\sim p(\mathcal T)}\frac 1 T\sum\limits_{t=1}^T||f_\theta(x_t^{(i)})-z^{proto}||_2^2$,通过最小化这个损失训练特征提取器,强制其生成的图像位于同一分布。
更具体的,文章给出了前向过程的伪代码如下图。对于训练,

快速适应性
对于学习得到的网络结构,在面对新的 $\cal Q,\ S$ 时,只需要按照同样的方式对 $\cal S$ 进行采样,输入已经初始化的 $f_\theta$,得到特征 $z$,对于特征 $z$ 输入已经预训练好的梯度生成器 $g_\psi$ 得到需要回传的梯度之一 $g_\psi(z)$,之二为分布损失回传的梯度,即 $\nabla_\theta\mathcal L_{proto}(\hat z,\hat z^{proto})$,用他们之和作为新的梯度来更新 $\theta$,这样就可以快速地适应新的数据集。同时对于 rPPG 估计器,其梯度不会更新,值也不会变化。
对于上述过程,其有效的假设在于:对于 ppg 信号的估计,其特征提取部分和从特征生成信号的部分是解耦合的。也就是说对于已经训练好的模型,面对新数据集时只需要修改特征提取器就可以使最终的结果正确。
对于学习新的 $\cal Q,\ S$,在学习过程中的伪代码如下图所示。对于适应性学习,训练的轮数为 10。

结果
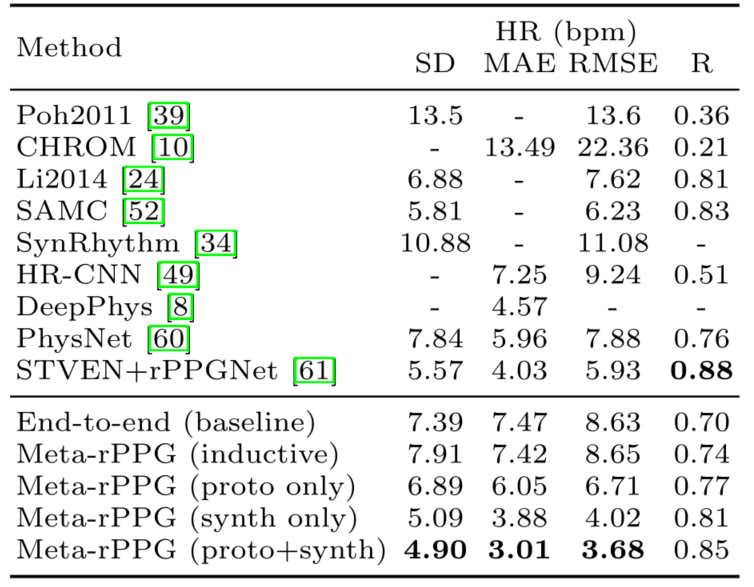
本文在 MAHNOB-HCI 和 UBFC 上测试了结果,使用含有 18 个长度为 120 秒的视频进行了预训练(没有给出预训练选择的数据集),和消融实验一起做成了一张表格如下图,这是 MAHNOB-HCI 的结果,是非常好的,在 physformer 中也没有明显的落后,并且其训练集小、适应性高。
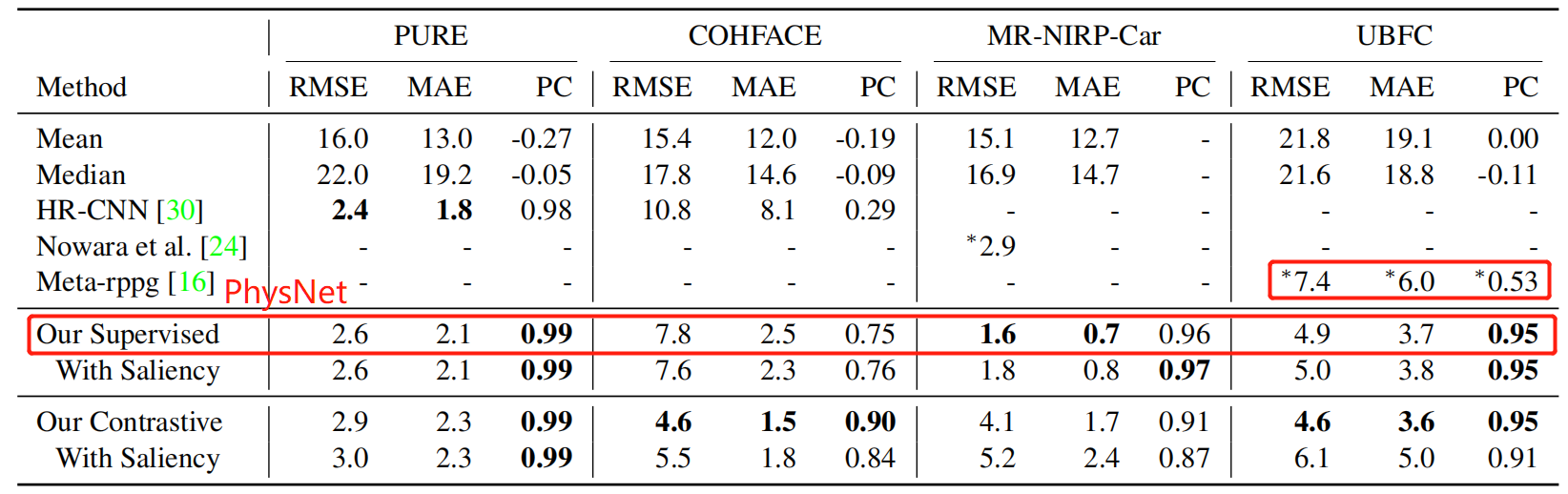
而在 UBFC 上的结果并不好,给个 The Way To My Heart 的结果可见一斑