Long-Tailed Multi-Label Visual Recognition by Collaborative Training on
Uniform and Re-balanced Samplings
【长尾识别】【ICCV2021】【paper】【code未开源】
摘要
本文提出了一种双分支网络,分别对均匀采样和重平衡采样的数据进行处理,对于每个网络的结果分别计算带有样本数先验的分类误差,同时为了消除两个网络可能针对自己的数据集产生的过拟合问题,提出了一种交叉损失使两个网络能够具备一致性的 bias。
概览
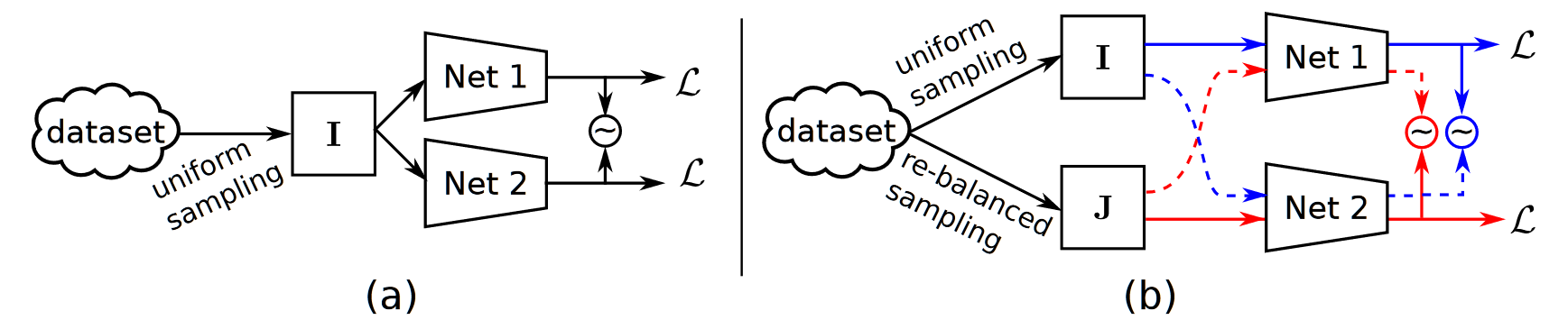
创新
- 一个双分支网络,同时使用均匀采样和 re-balanced 采样进行预测
- 一个新的一致性损失来约束双分支网络的一致性
- 一个仿照 focalloss 在 BCE 上的改进损失
网络
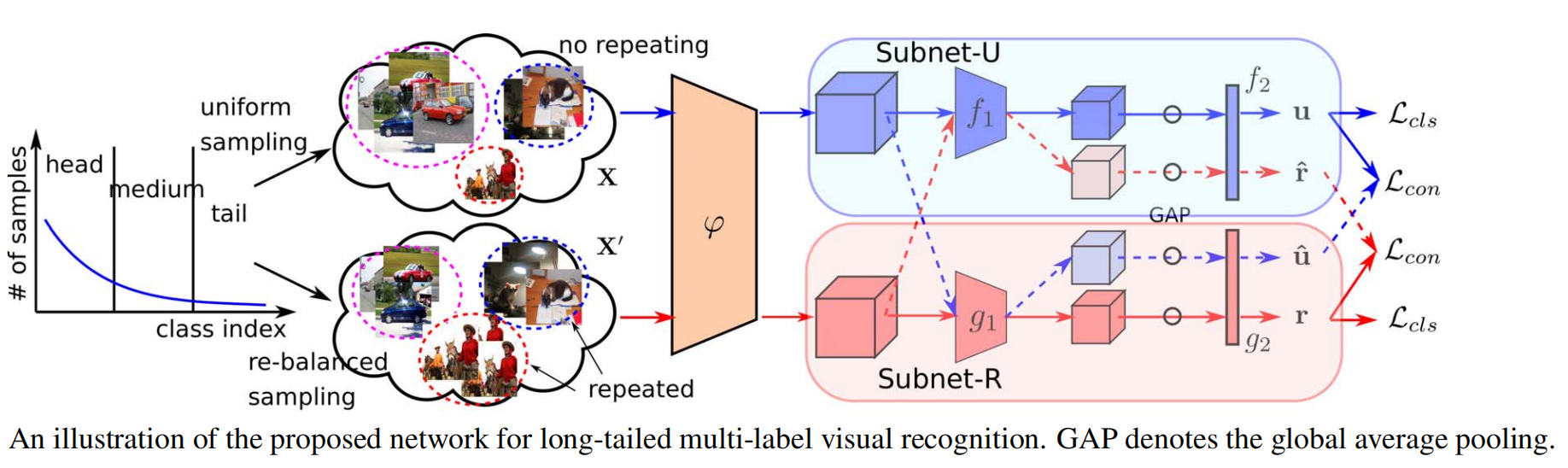
数据准备:首先对于数据集进行两种不同的采样,使用均匀采样(每个样本被选中的概率为 $\frac1N$)得到的训练集(共 $N$ 个)称为 $X$,使用 re-balanced 采样(即每个样本被选中的概率为 $\frac1K\cdot \frac 1{N_k}$,$K$ 表示数据集共有多少类别,$N_k$ 表示该样本所属类别的数目)得到的训练集称为 $X’$。对应的 label 分别为 $Y,Y’\in(N,K)$,每行对应一个 one-hot 向量。
网络前向:如上图所示的 $\phi$ 表示去掉最后一层的卷积 ResNet,$f_1,g_1$ 均表示 ResNet 的最后一层,但是不共享参数。$f_2,g_2$ 均表示由 MLP 组成的分类头,但是不共享参数。从 $X,X’$ 中的数据(分别随机采样的数据)首先统一进入 $\phi$,得到的特征分别进入两个分支,记进入 $f$ 分支的为 $x^u$,$g$ 的为 $x^r$。经过上下两个子分支之后共输出 4 个分类结果:
- $u=f_2(f_1(\phi(x^u)))$
- $\hat r=f_2(f_1(\phi(x^r)))$
- $\hat u=g_2(g_1(\phi(x^u)))$
- $r=g_2(g_1(\phi(x^r)))$
因此,可以简单地想到,$u,\hat u,y^u$ 应该一致,$r,\hat r,y^r$ 应该一致,分别计算 loss 即可。
损失
对于 $(u,y^u)$ 和 $(r,y^r)$,其约束的是每个分支正确预测对应类别概率的能力,因此采用分类损失计算:
其中,$i\in[1,N]$,$y_{ik}$ 表示第 $i$ 个样本是否为第 $k$ 个类别(0/1),$w_k=y_{ik}^ue^{1-\rho}+(1-y_{ik}^u)e^\rho,\ \rho=\frac{N_k}N$ ,$\sigma_k^p,\mu_k^p$ 分别表示第 $k$ 个类别正样本的方差均值,上标为 $n$ 的表示负样本。
简单理解为:
- $w_k $ 是一个 class/sample-ware 的参数,该类别的正样本越多,对错误的惩罚就越小
- 所谓正样本数就是属于该类别的样本 $N_k$,$\sigma_k^p,\mu_k^p$ 表示的是 $Y$ 中所有满足第 $k$ 个值为 1 的行组成集合的均值方差
- $u_{ik}\cdot\sigma_k^p+\mu_k^p$ 中的 $u_{ik}$ 是一个概率,属于 $(0,1)$,这样写而不是直接使用 $u_{ik}$ 可以再对由于正负样本数量不同产生的 bias 进行修正
- 整体的损失表示:当 $y_{ik}^u$ 为 1 时,$u_{ik}$ 越大越好,反之则越小越好;$w_k$ 使正样本多的类别权重减小;$u_{ik}\cdot\sigma_k^p+\mu_k^p$ 使正样本多的类别最终预测出的概率值偏低,负样本多的类别最终预测出的概率值偏高。
而对于 $(\hat u,u)$ 和 $(\hat r,r)$,其约束的是两个模型对同样的输入得到同样输出的能力(也就是限制模型对于数据的 bias):
这个损失很直观,就是两个模型对于同样的输入应该得到同样的输出。
最终的 loss 为:
$\lambda$ 是平衡权重的超参。
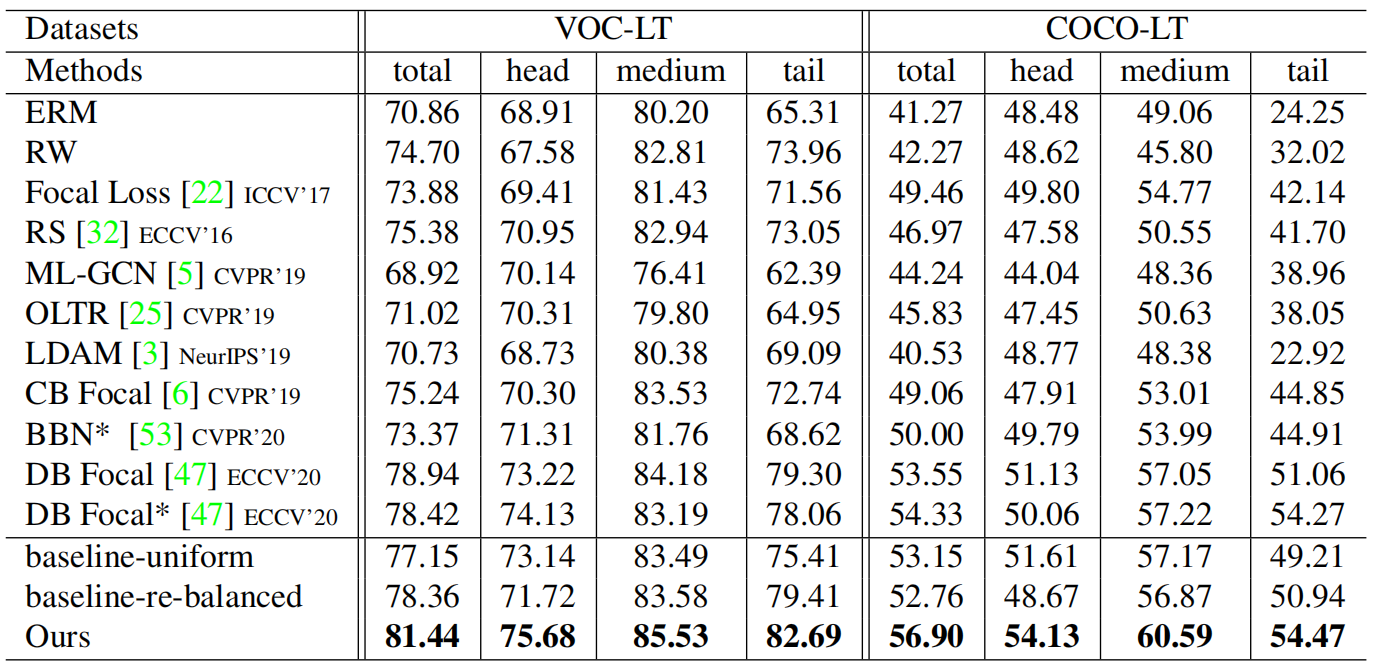
结果
- nonsense