diffusion theories
摘要
本文将承接上文的 DDPM,继续介绍其他的扩散模型理论,以及对扩散模型扩展的探索:
- SMLD(NIPS2019):Generative modeling by estimating gradients of the data distribution
- SDE(ICLR2021):Score-Based Generative Modeling through Stochastic Differential Equations
SMLD : Generative modeling by estimating gradients of the data distribution
前置说明
SMLD 全名为 Score Matching Langevin Dynamics,即基于分数匹配的郎之万采样方法,其主要提出了 NCSN。NCSN 全名为 Noise Conditional Score Network,即以噪声为条件的分数(预测)网络。本文提出了一种基于分数匹配的加噪-去噪过程,同时采用郎之万采样进行逐次迭代,是扩散模型的基础理论之一。
在阅读本方法时,最好一直带着三个疑问:1.为什么要向样本中添加噪声,2.噪声是怎么样被添加至样本的,3.噪声是如何被去除的。
- 什么是 score?
所谓的 score,定义为数据分布的对数的梯度。对于一个数据分布 $p(x)$,其 score 为 $\nabla_x\log p(x)$。这是数学上的定义,形象化地表示下,假如 $p(x)$ 如下图(左)所示,则其 score 如下图(右)所示。这个 score 的作用是方便采样,具体来说,假如从 $p(x)$ 某个随机位置开始采样,其初始值大概率没有在高密度位置,此时只需要按照梯度逐步前进,将会逐渐到达高密度区域。
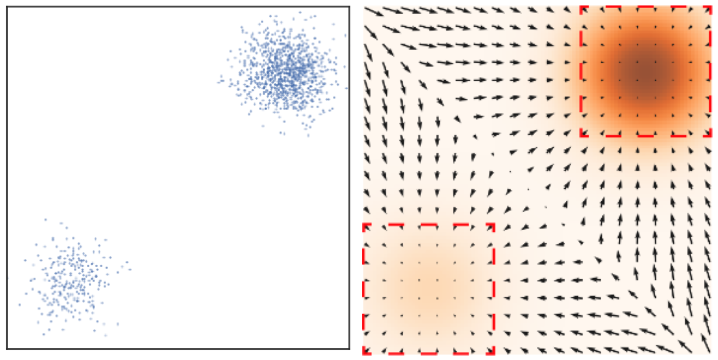
- 什么是 郎之万采样?
郎之万采样就是一种采样方式,其来源于郎之万动力学 Langevin dynamics,也就是扩散模型中去噪的迭代过程,具体来说,给出一个分布 $p(x)$ 的分数,对其的采样过程为:$x_t=x_{t-1}+\frac\epsilon2\nabla_x\log p(x_{t-1})+\sqrt\epsilon z_t$,其中,$\epsilon$ 表示步长,即每次走几步,$z_t\sim N(0,I)$ 表示标准正态分布(噪声),整个过程可以看做,对于初始点 $x_{t-1}$,下一步将在其基础上移动 $\frac\epsilon2$ 步的梯度,并且伴随一个低阶的噪声扰动。

优化设计(扩散-逆扩散过程)
低密度不准确问题
我们可以看出来,如果我们有一个非常准确的分数时就可以进行好的采样,但是估计分数也就是在估计分布,没有办法直观地进行获取,而是需要一个神经网络进行逼近,即 $\min\ E_{p(x)}[||s_\theta(x)-\nabla_x\log p(x)||_2^2]$。但是在估计分数时有着天然的问题(即使我们已知分布):当数据分布比较集中(方差较小)时,空间中会存在大量的低密度区域,在这些区域中没有足够的样本对分数进行估计。这种情况如下图所示:
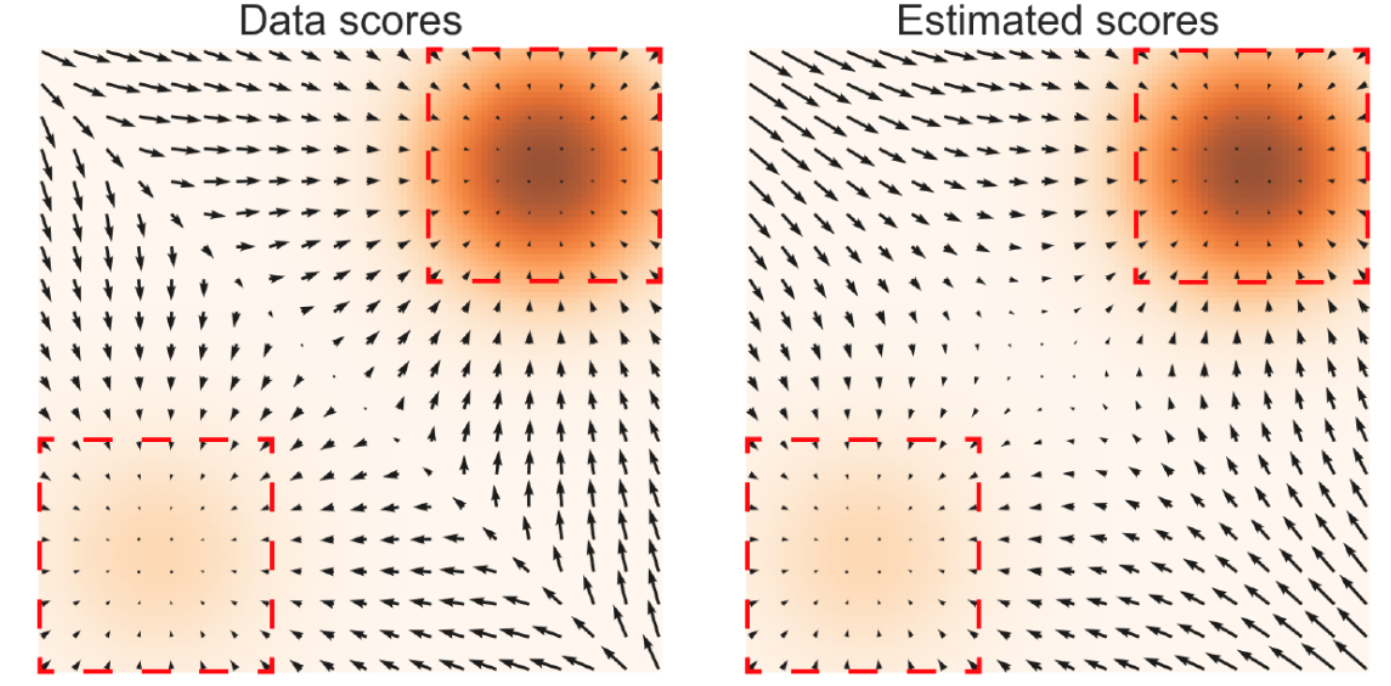
使用退火郎之万采样
本文额外引入了一个探讨:当目标数据分布是由两个不同的分布之和时,能否准确进行不同分布的采样?考虑这样一个混合分布:$p(x)=\pi p_1(x)+(1-\pi)p_2(x)$,其中 $\pi$ 为常数,则 $\nabla_x\log p(x)=\nabla_x\log p_1(x)+\nabla_x\log p_2(x)$,也就是说,虽然混合分布 $p(x)$ 本身与 $\pi$ 有关系,但是其 score 却与 $\pi$ 无关,这将极大地限制从混合分布中进行正确采样。
本文进行了这样的实验:用不同的方法从混合高斯分布中获取样本。(a) 精确抽样。(b) 使用精确分数的郎之万采样进行抽样。(c)使用退火郎之万采样进行抽样。显然,朗之万动力学不正确地估计了两种模式之间的相对权值,而退火朗之万动力学则忠实地恢复了相对权值。
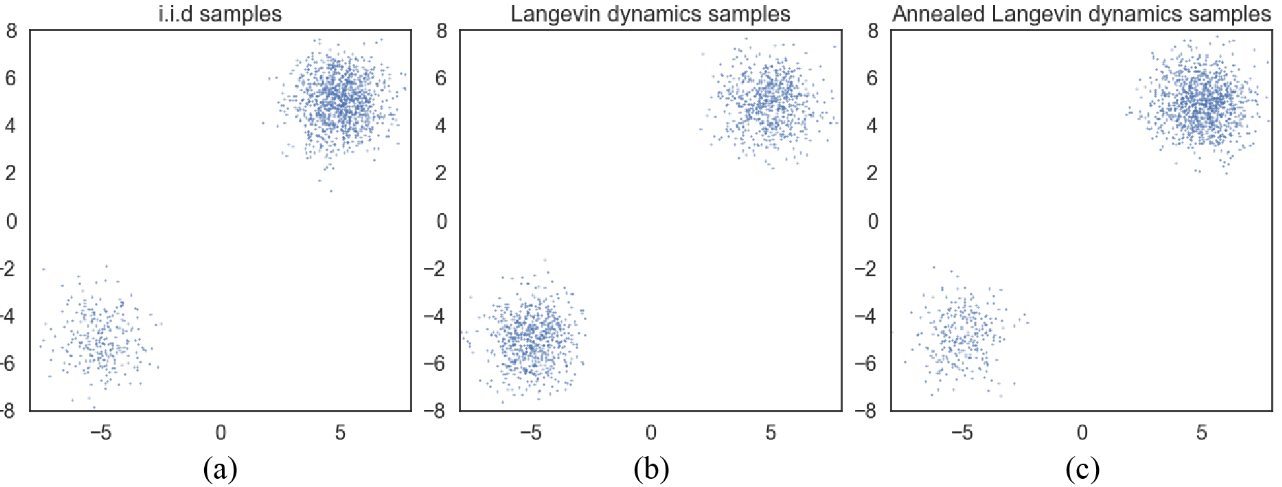
NCSN:加噪与训练
- 加噪方式
既然我们已经明确在分布集中时难以准确估计 score,那么我们就要对其进行加噪,通过使其具备更广的分布从而能够准确估计 score,这也就回答了第一个问题。但是这也会带来一些额外的问题:加入了较大的噪声之后,我们估计出的分布将会和真实分布差距较大。
为了解决加噪之后难以去除的问题,我们通过这样的方式加入噪声:预设一个公比小于 1 的等比数列 $\{\sigma_i\}_i^L$,将其每一项分别作为正态分布的噪声 $N(0,\sigma^2I)$ 加入原始数据分布 $p(x)$ 之中以获取新数据分布 $q_\sigma(\tilde x)$,则 $q_\sigma(\tilde x)\sim\int p(x)N(\tilde x|x,\sigma^2I)dx$。此时我们的目的就是利用分数估计网络逼近 $q_\sigma(\tilde x)$,不过此时我们将对应的方差 $\sigma$ 也输入至分数网络之中:$s_\theta(\tilde x,\sigma)\simeq \nabla_{\tilde x}\log q_\sigma(\tilde x)$。
这种加噪方式很好地平衡了上述两个难题,通过先加入大噪声使数据分布更广泛,从而获取原本低密度区域的正确分数估计,再逐步缩小加噪方差,直至最终可以收敛到和原数据分布基本一致。这种以 $\sigma_i$ 作为条件的分数估计网络就称为 NCSN。
- 训练方式
在训练的过程中,由于 $\sigma$ 总共有 $L$ 个,那么计算 loss 时自然所有的都需要考虑在内,为了推理出整体形式,首先考虑对于某一个 $\sigma\in\{\sigma_i\}_i^L$
因此若考虑全部的 $\sigma$,损失函数应该写为:$L(\theta;\{\sigma_i\}_i^L)=\frac1L\sum\limits_{i=1}^L\lambda(\sigma_i)L(\theta;\sigma_i)$。其中,$\lambda(\sigma_i)$ 用于平衡各个方差之间的数量级,在合理的假设下,平衡之后的损失应当不受到 $\sigma_i$ 的级数的影响。作者指出在训练到收敛之后 $|s_\theta(x,\sigma)|_2\propto \frac1\sigma$,因此设 $\lambda(\sigma_i)=\sigma_i^2$,以此消除由 $\sigma$ 数值带来的影响。
NCSN 的推理过程
使用退火郎之万采样对数据进行多次迭代,具体来说,当 score 被近似正确估计时执行下列步骤。其关键的见解在于:将 $\sigma$ 从大到小进行迭代,大的 $\sigma_i$ 可以使低密度区域更少,但逼近 $p(x)$ 效果不好,尽管如此,以此为 score 进行 $x_t$ 的郎之万采样也会大致地向高密度区域前进。通过这种方式,尽管大的 $\sigma_i$ 不够精确,但足以使 $x_{t+1}$ 进入 $\sigma_{i+1}$ 的 score 准确估计区域。

SDE : Score-Based Generative Modeling through Stochastic Differential Equations
前置说明
所谓 SDE,即随机微分方程(Stochastic Differential Equations),常用来对随机过程进行建模,对于微分方程来说,常微分方程 ODE 的一般形式为:$dy=f(x)dx$,通常可以使用对 $dx$ 积分的方式求解 $f(y)$,随机微分方程 SDE 的一般形式为:$dx_t=f(x_t,t)dt+g(x_t,t)dw_t$,其中 $w_t$ 表示随机项。本文旨在使用 SDE 构造出一个一致性的扩散模型 pipeline,以指导后续的扩散模型构造。
加噪过程
当噪声尺度的数量接近无穷大时,我们基本上会随着噪声水平的不断增加而扰乱数据分布。在这种情况下,噪声扰动过程是一个连续时间随机过程,如下所示
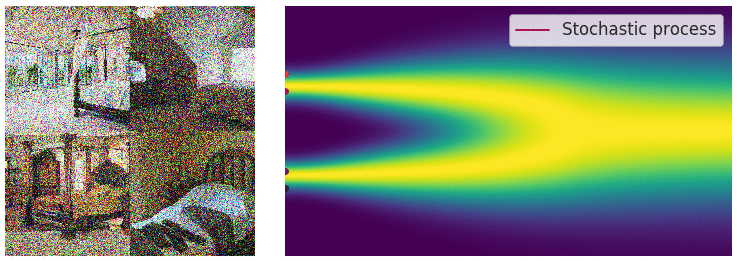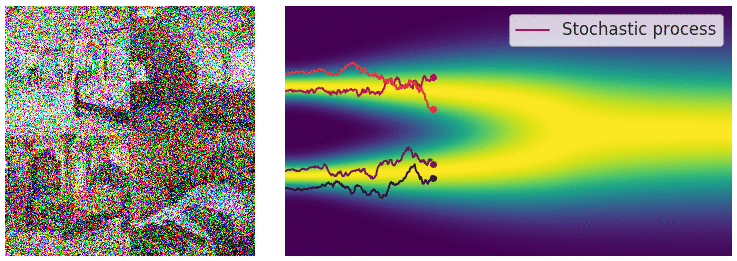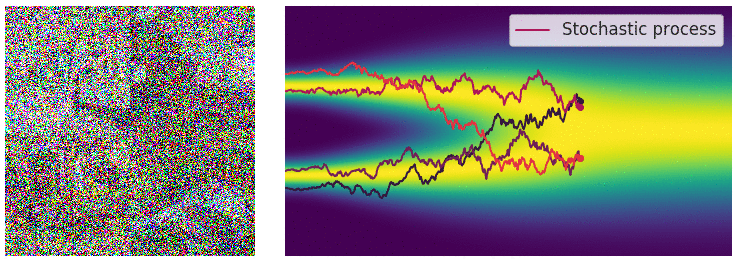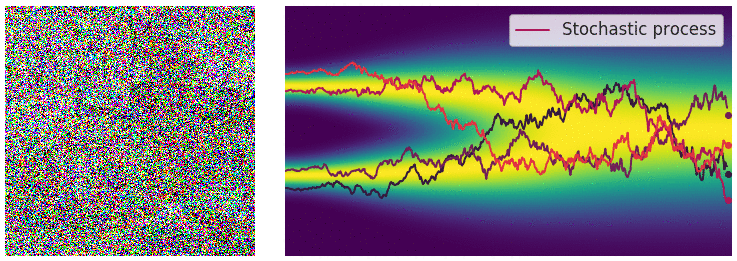
这个过程使用 SDE 描述为
其中,作者将 $f(*,t)$ 称为漂移系数,$g(t)$ 称为扩散系数,对于一个 $dt$ 内的 $dx$,前半部分描述了一个确定的移动,后半部分则表示了一个噪声,在单位时间 $dt$ 内的 $dx$ 变化如下图所示:
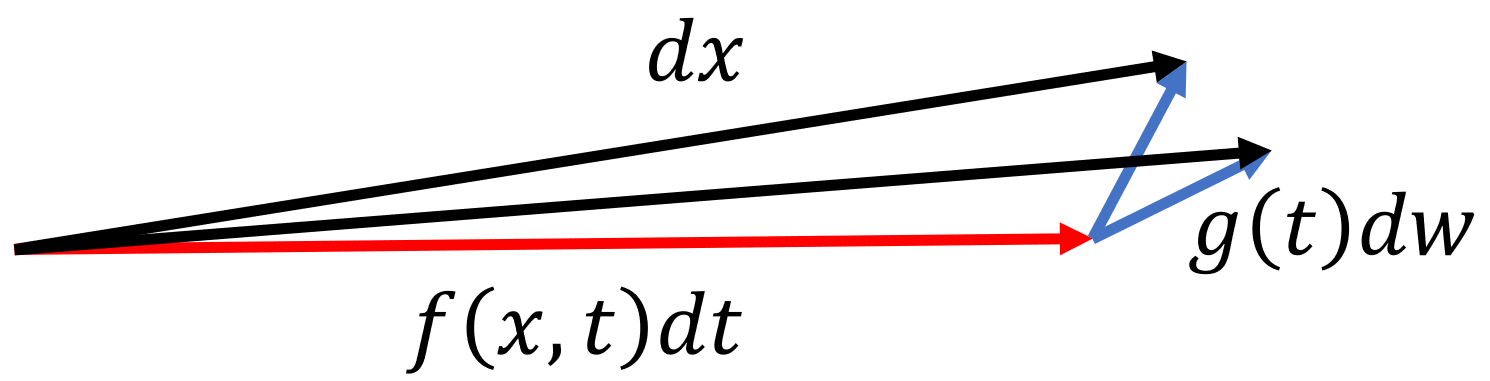
在上式中,SDE 的具体形式(指 $f(x,t),\ g(t)$ 的表达式)是手工设计的,接下来我们将首先探索一下不使用具体形式的抽象化推理,然后将给 $f(x,t),\ g(t)$ 赋值具体表达式并以此推理出 DDPM 与 SMLD 两种具体扩散模型。
去噪过程
在有限数量的噪声尺度下,我们可以通过使用退火 Langevin 动力学反转扰动过程来生成样本,即,使用 Langevin 动力学从每个噪声扰动分布中顺序采样。对于无限噪声尺度,我们可以通过使用反向 SDE 类似地反转样本生成的扰动过程。
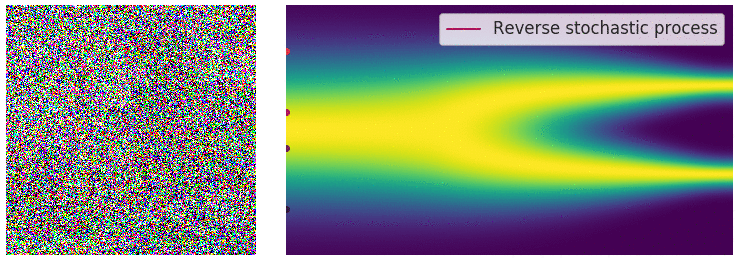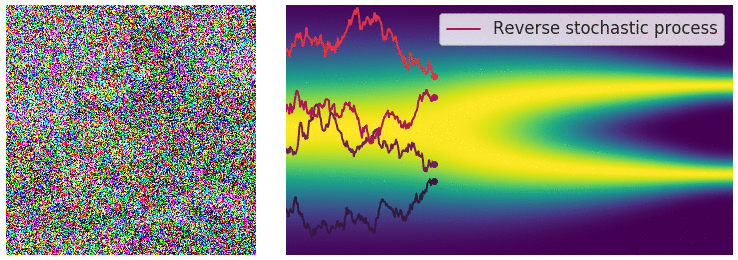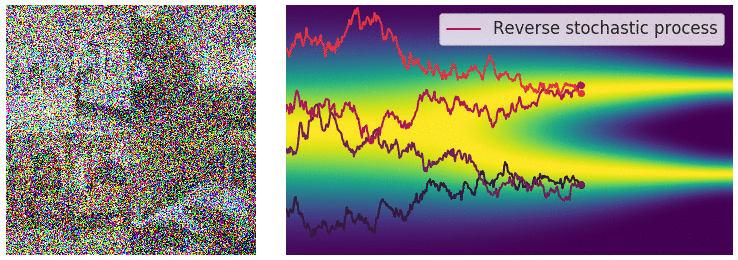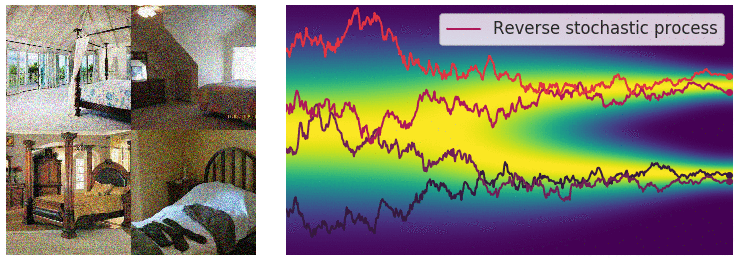
为了能够得到逆向过程的 SDE 方差,我们需要对正向过程 $dx=f(x,t)dt+g(t)dw$ 进行推理,推理过程如下:
首先,离散化扩散过程 SDE,$dx=x_{t+\Delta t}-x_t,\ dt=\Delta t$,得到:
这里有两个需要注意的点:1.在函数 $f$ 内,$x\to x_t$ 而非 $x_{t+\Delta t}$ 是因为这里我们是扩散过程,是给出 $x_t$ 求 $x_{t+\Delta t}$ 的过程;2.扩散项的 $dw$ 变成了 $\sqrt{\Delta t}\epsilon$,这个$\Delta t$ 加根号是结论性的,有非官方的解释。
由上式可得
为了进行逆扩散过程,我们需要知道 $p(x_t|x_{t+\Delta t})$ 因此可以列出贝叶斯公式
若此时将式 $2$ 代入式 $3$,则会保留一项 $\frac{p(x_t)}{p(x_{t+\Delta t})}$ 无法消去,因此先尝试处理此项
对 $\log p(x_{t+\Delta t})$ 在 $x_t$ 处进行泰勒展开,得
- 需要注意的是,在上式展开时应采用多元泰勒展开方式进行,不然可能会漏掉最后一项(漏不漏不影响结果就是了)
将式 $5$ 代入式 $4$,得
因此将式 $2$ 和式 $6$ 一起代入式 $3$,即可得到
在 SDE 扩散模型的假设中,$\Delta t\to0$,不难看出上式具备 $\mathcal O(1/\Delta t),\ \mathcal O(1),\ \mathcal O(\Delta t)$ 的部分,因此可以令 $\mathcal O(\Delta t)$ 的部分约去,同时以 $x_{t+\Delta t}-x_t$ 为一个整体 $\Delta X$,可以将 $7$ 化简为
对上式进行配方,然后去掉 $\mathcal O(\Delta t)$ 可得
此时,由于我们应该从输入 $x_{t+\Delta t}$ 得到 $x_t$,在保证正确性的情况下(因为 $\mathcal O(\Delta t)\to 0$)对式 $9$ 进行简单的换元
将此式变换为正态分布可以写成
写成离散形式的 $x_{t+\Delta t}$ 与 $x_t$ 的关系为
将式 $12$ 写为微分形式为
由此,我们就得到了逆扩散过程的 SDE 公式。为了计算反向 SDE,我们需要估计 $\nabla_x\log p(x_t)$,为此,我们训练一个基于时间依赖分数的模型 $s_\theta({x}, t)$,这样 ${s}_\theta({x}, t) \approx \nabla_{x} \log p_t({x})$。这类似于基于噪声条件分数的模型 ${s}_\theta({x}, i)$ 用于有限噪声。
我们的训练目标 $s_\theta({x}, t)$ 是 Fisher 散度的连续加权组合,由下式给出
其中,$\mathcal{U}(0, T)$ 表示时间间隔内的均匀分布 $[0,T]$, $\lambda: \mathbb{R} \to \mathbb{R}_{>0}$ 是正加权函数。通常我们使用 $\lambda(t) \propto 1/ \mathbb{E}[| \nabla_{\mathbf{x}(t)} \log p(\mathbf{x}(t) \mid \mathbf{x}(0))|_2^2]$ 以平衡不同分数匹配损失随时间的大小。由此便可以展开训练。
VP-SDE 和 VE-SDE
对于原始式子式 $1$,当我们令 $f(x,t)=0,\ g(t)=\frac{d}{dt}\sigma_t^2$ 时,SDE 被称为 VE(方差爆炸)SDE,也就对应着 SMLD 分数扩散模型,由此可以推出 VE-SDE 的更新公式为:$x_{t+\Delta t}=x_t+\sqrt{\sigma_{t+\Delta t}^2-\sigma_t^2}\epsilon$。
对于原始式子式 $1$,当我们令 $\{\bar\beta_i\}_1^T=\{T\beta_i\}_1^T$,$\beta(\frac iT)=\bar\beta_i$,$f(x,t)=-\frac12\beta(t)x_t,\ g(t)=\sqrt{\beta(t)}$ 时,SDE 被称为 VP(方差收缩)SDE,也就对应着 DDPM 去噪扩散模型,由此可以推出 VP-SDE 的更新公式为:$x_{t+\Delta t}=\sqrt{1-\beta_{t+\Delta t}}x_t+\sqrt{\beta_{t+\Delta t}}\epsilon$。