CodeFormer

Towards Robust Blind Face Restoration with Codebook Lookup Transformer

【盲人脸重建】【NIPS2022】【paper】【code】

摘要

  本文借鉴 VQGAN 的思想细化了其应用领域并进行了启发式的改造，将条件生成限制到盲人脸重建，通过增加 CFT 模块优化过度平滑的问题，并且将采样器去掉，作为必选项在重建图像时优化隐编码。由于 CFT 模块可选，因此在一定程度上避免了如 GPEN 的跳跃连接，防止过差的 LQ 影响重建质量。其本质与其说参考了更多的盲图重建工作，倒不如说参考了 VQ 系列的工作。

概览

---

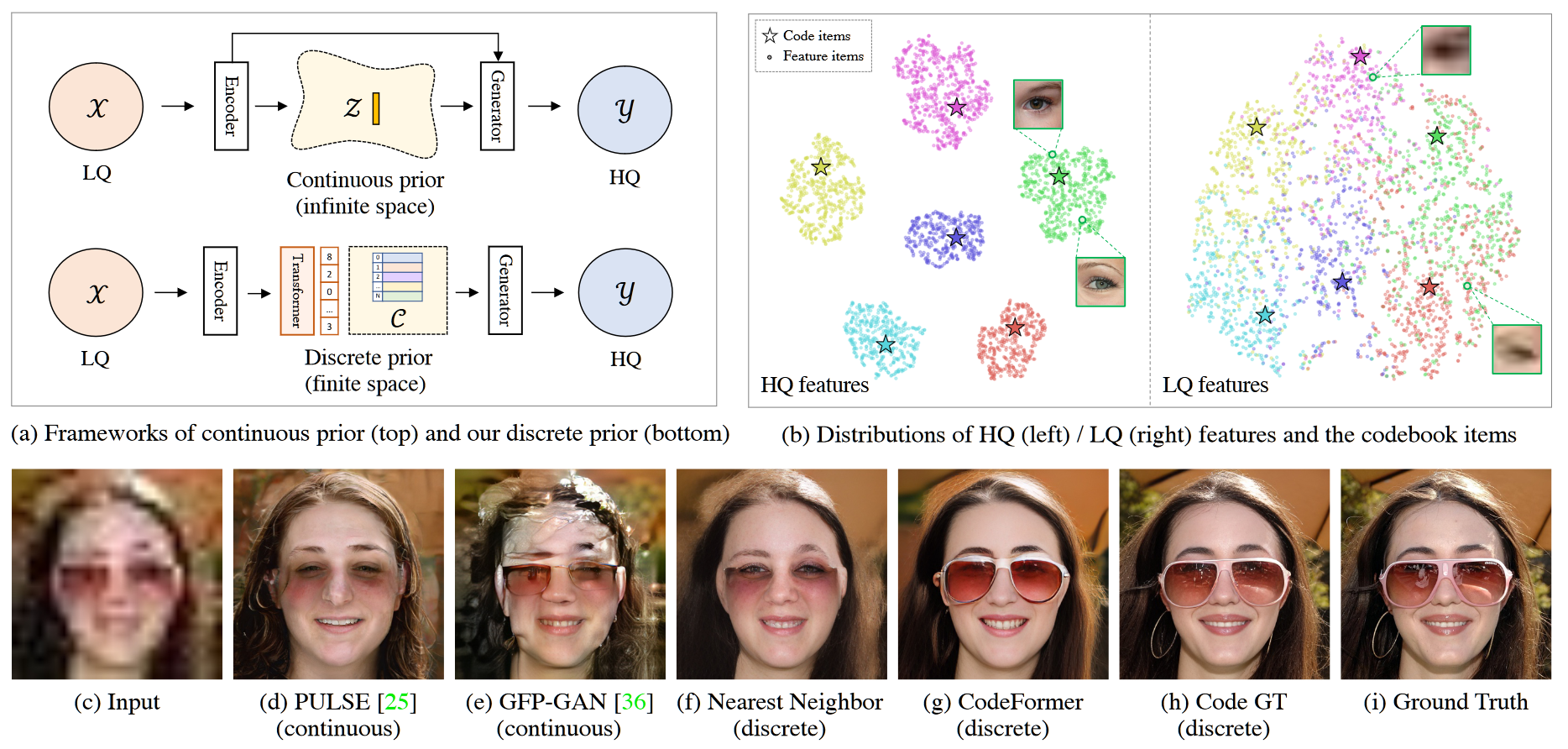
前置知识

VQVAE

Neural Discrete Representation Learning NIPS2017

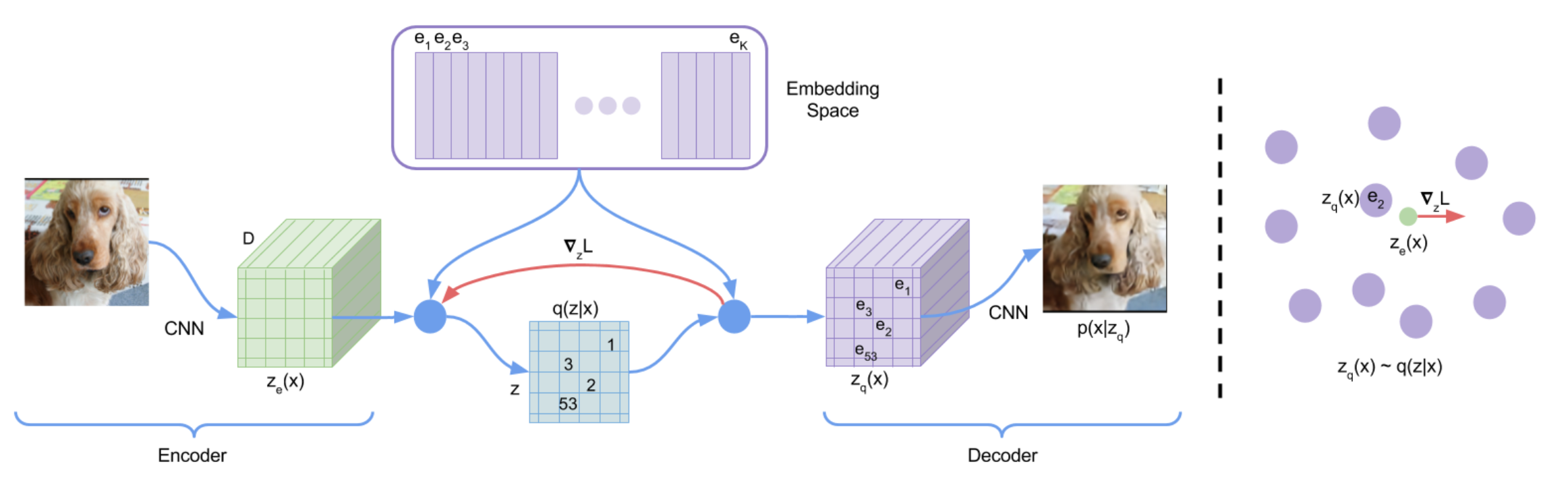
  所谓 VQVAE，即矢量量化（Vector Quantized）VAE，其基础仍是 VAE，其具备和 VAE 基本一致的训练过程，只是在 Encoder $q$ 编码出 latent code $z_e$ 之后并不直接给 Decoder，而是经过通过一个码本 CodeBook 进行量化，得到离散的编码表示 $z_q$，再输入 Decoder $p$ 生成重建图像 $p(x|z_q)$。

  首先，论文本身上，其区别于 VAE，基于量化的编码可以很好地避免隐空间在采样重建时出现崩溃，但是同时由于 codebook 的限制，采样的多样性也相应减弱了，这种量化的思想更适用于重建（生成）质量大于多样性的场景，比如盲图重建。对于原文来说，VQVAE 主要进行图像重建、条件生成、语音生成，其中重建效果甚至不如好的 AE，条件生成结果更是和 CGAN 比不了，更不用提最近的 GAN。语音重建是 VQVAE 卖点之一，其宣称自己证明了深度学习模型可以无监督地从音频里学到语义。和盲图重建无关，就不展开了。

backbone

  codebook 和量化过程可以描述为：

• codebook 实际上是向量的集合，其 shape 为：$(m\cdot n)\times d$ ，其中 $m,\ n,\ d$ 是原图经过编码器得到的隐编码 $z_e$ 的 shape
  • 该集合有 $m\cdot n$ 个元素，每个元素是连续的 $(1,d)$ 的向量，元素下标范围是 $[0,m\cdot n)$，必须为整数
  • codebook 中每个元素的初始值随机生成，在训练的过程中不断优化，优化目标是量化过程中损失最少的信息
• 量化过程为：
  • 对于编码器的输出 $z_e\to(m,n,d)$，对其中的 $z_e[i,j]$ 有：
    • $z_q[i,j] = e_k,\ \ where\ \ k=arg\min_j||z_e[i,j]-e_j||_2$，从而输出 $z_q\to(m,n,d)$

  其网络训练过程主要可以被描述为：

• 正向传播
  • 输入原图 $x$，经过编码器 E 得到 $z_e$
  • $z_e$ 和 codebook 进行最近邻查询，将 $z_e$ 量化为 $z_q$
  • $z_q$ 经过解码器 D 得到重建图像 $p(z_q)$
• 反向传播
  • $L=\log p(x|z_q(x))+||sg[z_e(x)]-e||_2^2+\beta||z_e(x)-sg[e]||_2^2$
  • 其中，第一项为重建损失，也是 VAE 的 ELBO 中的一项，使用 L1 或者 L2 损失度量重建图像质量
  • 第二项和第三项为优化量化过程中的信息损耗，其中 $sg$ 表示 detach，即分别优化编码器 E 和码本 codebook

  相对于 VAE 来说，ELBO 缺少了 KL 散度的度量项，这是因为 $z$ 并非高斯分布，实际上，$z$ 的分布是离散的分类分布，具体可以描述为：

$$q(z=k|x)=\begin{cases} 1\ \ \ \ \rm{for} \ k=arg\min_j||z_e(x)-e_j||_2\\ 0\ \ \ \ \rm{otherwise} \end{cases}$$

  以此分布推理 KL 散度可以得到最终的结果为 $\log K$，$K=m\cdot n$。

从分类分布中采样

  对已经训练好的 backbone，按照 VAE 的思路接下来只需要使用解码器 $p$ 然后从高斯分布中采样隐编码 $z$ 就可以了，但是明显可以看到，$z$ 并不属于高斯分布，因此需要额外构建一种采样方式，本文采用的方式为 PixelCNN。

  PixelCNN 是自回归模型的一种，事实上使用任意一种自回归模型均可。所谓自回归模型，即模型接收当前位置前的序列并预测当前位置的值，类似于语言生成。对于 PixelCNN，具体的实现方式为采用卷积的方式进行 mask。

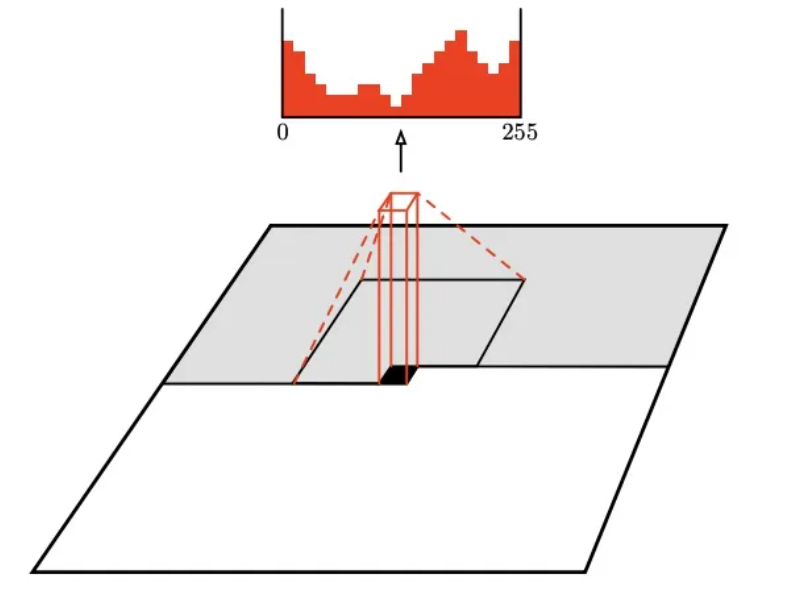
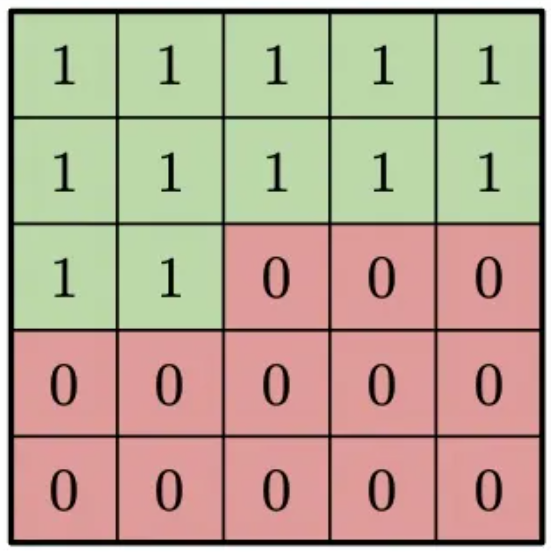
  上图表示了卷积核的卷积过程，对于黑色位置，卷积核只能看到灰色区域内的像素点，得到红色的像素分布并以此预测黑色位置像素，卷积核具体设计为下图：

  因为之后再 VQGAN 之中 PixelCNN 就使用 GPT-2 的 transformer 架构代替了，因此不再专门精读 PixelCNN。

  下图展示了使用 IN 训练的 PixelCNN 和 VQVAE 以不同的类别采样的结果，可以看到还是比较差的，只能说是初具雏形。

VQGAN

Taming Transformers for High-Resolution Image Synthesis CVPR2021

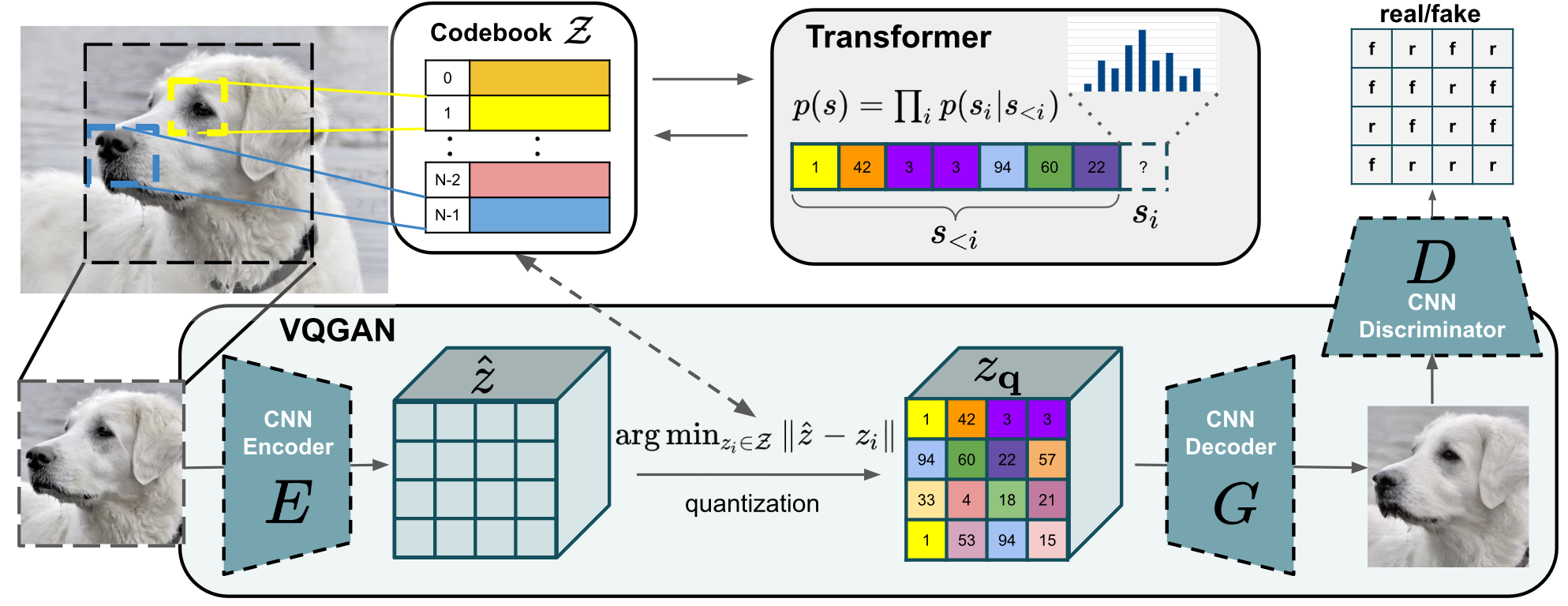
  VQGAN 针对 VQVAE 进行了两方面的改进：

• 在原本的 AE 大框架下加入了判别器 D
• 使用 transformer 架构代替了 PixelCNN

  相对于 VQVAE，VQGAN 在训练阶段只是多了一个 GAN 损失，其中量化损失描述为：

$$L_{VQ}(E,G,Z)=||x-\hat x^2||^2+||sg[E(x)]-z_q||_2^2+||sg[z_q]-E(x)||_2^2$$

  其中，第一项 MSE 即为重建损失 $L_{rec}$，后两项和 VQVAE 一致。

  VQGAN 对抗（交叉熵损失）损失描述为：

$$L_{GAN}(\{E,G,Z\},D)=\log D(x)+\log(1-D(\hat x))$$

  总损失描述为：

$$L_Q=arg\min_{E,G,Z}\max_D\mathbb E_{x\sim p(x)}[L_{VQ}+\lambda L_{GAN}]\\ \mathrm {where}\ \ \lambda=\frac{\nabla_{G_L}[L_{rec}]}{\nabla_{G_L}[L_{GAN}]+\delta}$$

  其中，$\nabla_{G_L}$ 表示损失关于 G 的最后一层的梯度，$\delta=10^{-6}$。

  对于采样部分，transformer 的训练方式为：对已经量化的序列进行预测，使用交叉熵函数学习如何把 codebook 映射到合理的分布，假设量化之后的序列为 $s$，则 transformer $p$ 预测序列 $s$ 可以表述为： $p(s)=\Pi_ip(s_i|s<i)$，训练损失描述为：

$$L_{transformer}=\mathbb E_{x\sim p(x)}[-\log p(s)]$$

  即对所有的 $x$ 采样之后预测出所有的 codebook 序列。

  需要注意的是，对于 VQGAN，其 transformer 需要预测的序列仍然较长，为了能够生成更高分辨率的图像，需要对 transformer 进行滑动窗口的方式进行预测，其示意图如下：

创新

• 基于 transformer 的全局感知能力保证了更好的重建质量和保真度
• 可控特征变换模块，以此解决 codebook 带来的多样性降低问题

网络

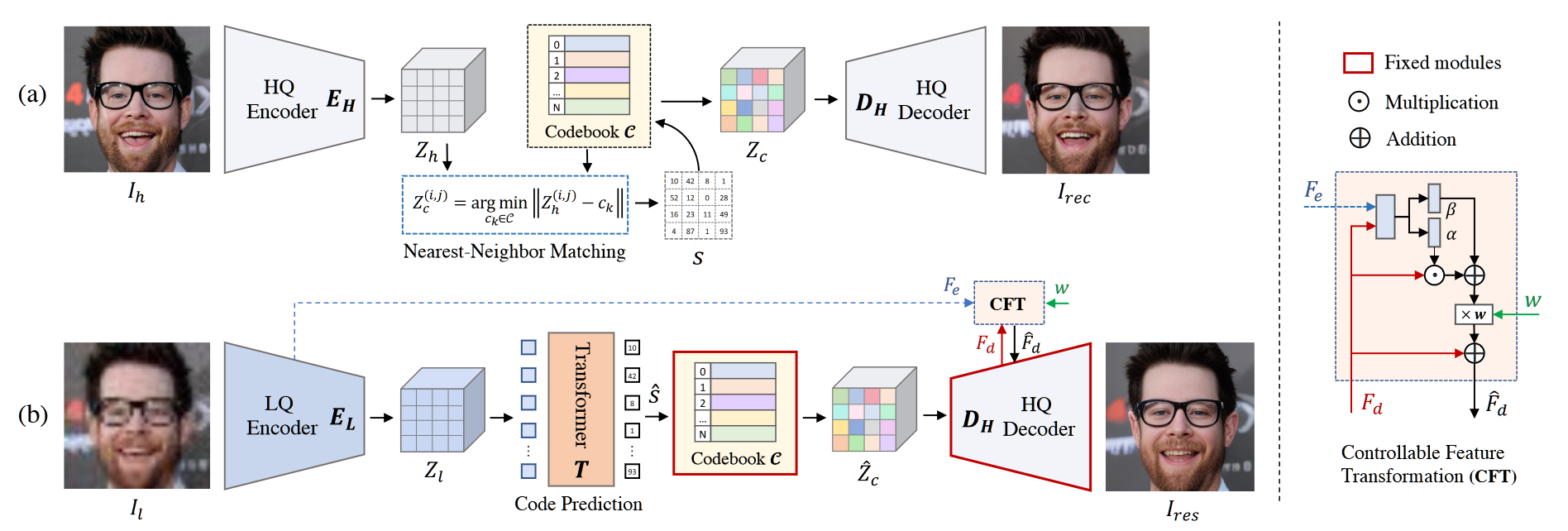
  在本文中，一些符号被重新命名，HQ 输入图像记为 $I_h$，编码器，解码器，判别器分别为 $E,\ G,\ D$，通过编码器之后的隐编码记为 $Z_h\in\mathbb R^{m\times n\times d}$，码表记为 $\mathcal C =\{c_k\in\mathbb R^d\}_{k=0}^N$，量化之后的隐编码记为 $Z_c\in\mathbb R^{m\times n\times d}$，量化之后的码表下标序列为 $s\in\{0,…,N-1\}^{m\cdot n}$，通过解码器之后的重建 HQ 图像记为 $I_{rec}$。

  整个网络结构很好理解，类比于 VQGAN，采用了三阶段的训练方式，第一阶段训练 VQVAE，如上图 (a) 所示，训练的损失函数为：

$$L_{codebook}=L_1+L_{per}+L_{code}+\lambda_{adv}\cdot L_{adv}$$

  其中，$L_1$ 是重建损失，使用 L1Loss，$L_{per}$ 是感知损失，使用 VGG19 计算，$L_{code}$ 是码表量化损失，按照 $||sg[Z_h]-Z_c||_2^2+\beta||sg[Z_c]-Z_h||_2^2$ 计算，$L_{adv}$ 是对抗损失，按照 $\log D(I_h)+\log(1-D(I_{rec}))$ 计算，$\lambda_{rec}=0.8$。

  第二阶段训练 transformer，具体来说，将 LQ 的输入 $I_l$ 进入编码器之后的隐编码 $Z_l\in\mathbb R^{m\times n\times d}$ 拉平为向量 $Z_l^v\in\mathbb R^{(m\cdot n)\times d}$，然后输入标准的 transformer 结构，位置编码使用 sin 相对编码，预测出的结果为用于重建 HQ 图像的 codebook 下标序列 $\hat s$，训练过程的损失函数为：

$$L_{tf}=\lambda_{s}\cdot L_{s}+L_{code'}$$

  其中，$L_s$ 即为预测出的 $\hat s$ 和真实 HQ 图像的量化序列 $s$ 的交叉熵损失，$\sum\limits_{i=0}^{mn-1}-si\log(\hat s_i)$，$L_{code’}$ 即为在 LQ 预测下的量化损失，其只用来优化 $E_L$，$L_{code’}=||Z_l-sg[Z_c]||_2^2$。

  编解码器由 12 个残差模块和 5 个上下采样模块组成，因此压缩比为 $32^2$，对于 codebook，$N=1024,\ d=256$，这个序列长度允许使用 transformer 直接进行全局建模。

  第三阶段参照 SFTGAN 的 SFTlayer 设计，具体如上图所示，其中淡淡色的方块是卷积的组合，$\alpha,\ \beta$ 相当于 SFT 的 $\gamma,\ \beta$，相当于 style，通过乘和加的操作实现了仿射变换，即风格嵌入，这些淡淡色的方块的目标即为融合 $F_e$ 和 $F_d$ 的风格。

  第三阶段的训练过程是在已经训练好的二阶段模型上进行微调，前向过程中调整的是解码器 $D_H$ 每一层的特征，具体来说对于某个层的特征 $F_d$，有，$\hat F_d=F_d+(\alpha\odot F_d+\beta)\times w$，其中 $\alpha,\beta=\mathcal {P}_\theta(c(F_d,F_e))$，其中，$\cal P$ 表示一系列的卷积组合。其损失函数是一二阶段的损失函数之和（除去和 code 相关的部分），梯度回传时更新除了码表之外的全部。

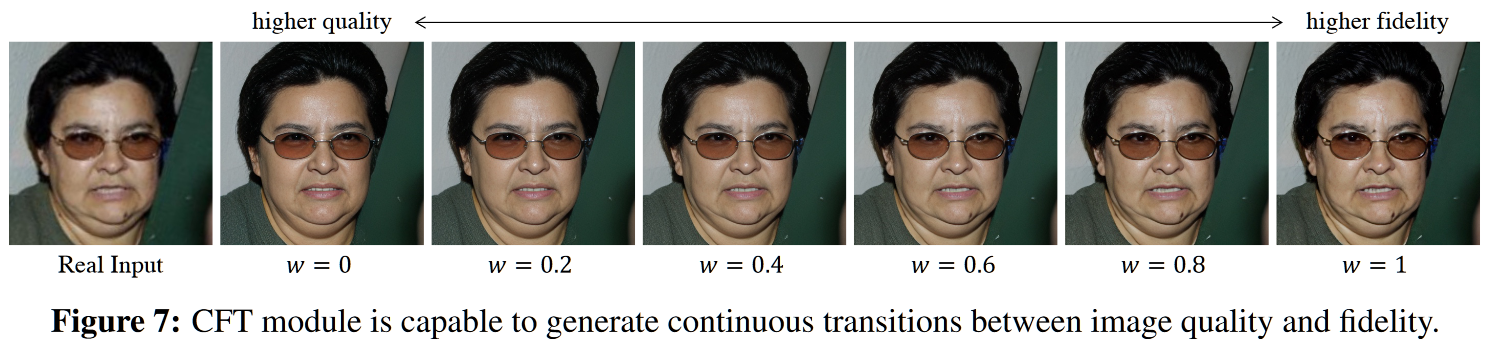
  在训练的过程中全部设置 $w=1$ 以保证模型学习到融合特征的能力，在推理的过程中设置 $w=0$ 能够最好地保证重建质量，在 $[0,1]$ 之间的调整则可以产生连续变化的生成结果，增加了多样性。

结果

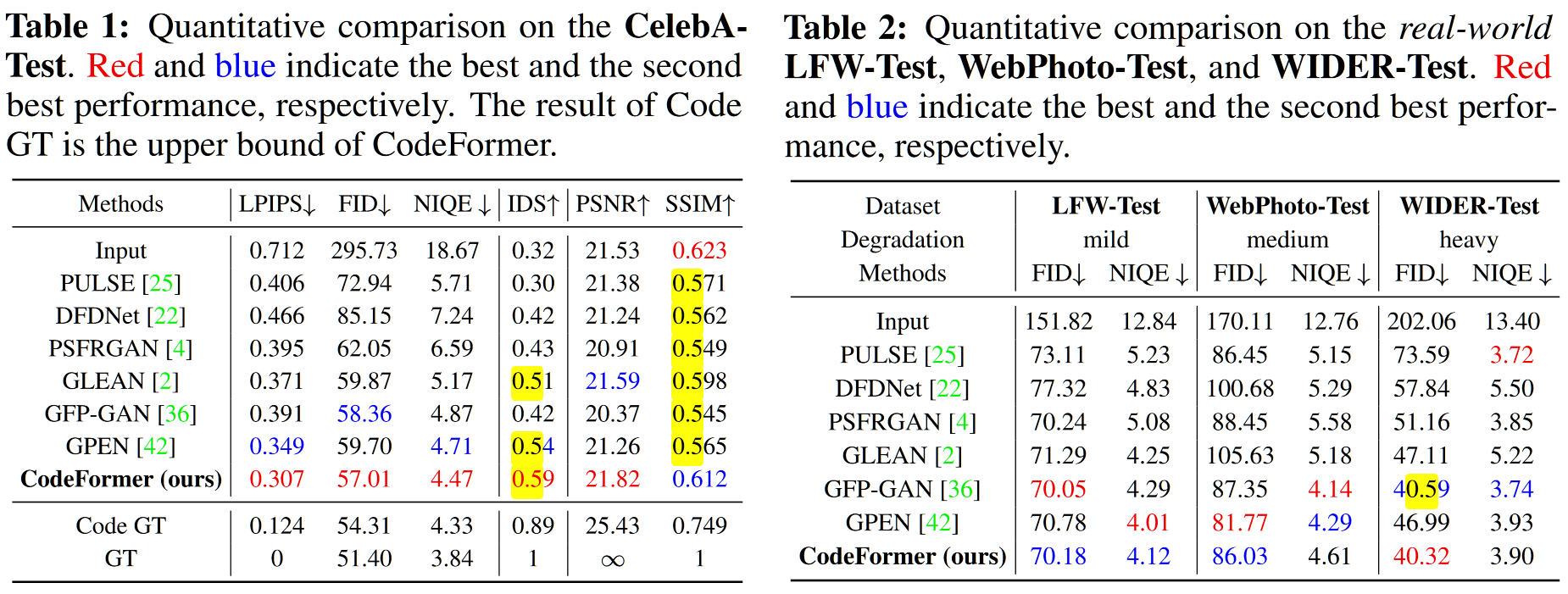
  本文首先在 Celeb-A，LFW，WebPhoto，WIDER 数据集上分别测试了性能，以 LPIPS，FID，NIQE，IDS，PSNR，SSIM 作为指标显示了模型优越的性能，对比的模型中不包括 VQGAN

  另一方面本文测试了和 VQGAN 在预测 codebook 序列上的正确性，由于 transformer 结构，准确度提升了很多（但是这里的 transformer 就是普通的 transformer，是否可以针对 transformer 的架构进行改进？）

  最后本文还论证了在第二阶段锁定解码器的必要性，通过测试是否在第二阶段更新解码器，得出结论：在第二阶段微调解码器会破坏学习到的先验知识。然后将本文的网络应用于了人脸图像修补，人脸图像上色等任务，同样取得了不错的结果。