BoxSnake: Polygonal Instance Segmentation with Box Supervision
【segmentation】【ICCV2023】【paper】【code】
abstract
本文首次仅使用 box-level anno 监督 polygon-level 分割,在假设(1.物体边界通常有像素变化;2.在物体 box 的邻域内,物体内外区域像素应分布均匀)成立下,提出了针对两个假设进行约束的损失函数,使 box-level 的分割可以细化至 polygon-level 的分割。
overview
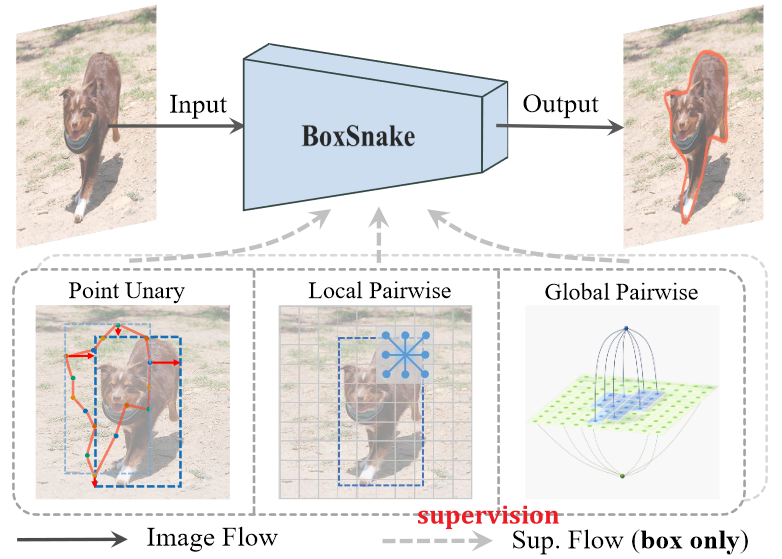
contribution
- 首次仅使用 box-level 监督模型进行 polygon-level 的分割预测
- 提出 local pairwise loss 用以约束 instance 边缘的像素变化
- 提出 global pairwise loss 用以约束 instance 内外的像素分布均匀(仅考虑 box 领域内)
formulation
输入图像 $\mathcal{I}\in\mathbb{R}^{H\times W\times3}$,其像素点集合记为 $\Omega_{\mathcal{I}}$;模型将会对 $N$ 个物体预测 $N$ 个多边形集合,每个多边形集合为 $\mathcal{C}=\{(x_i,y_i)\}_{i=1}^K$ 表示每个多边形由 $K$ 个点组成。
framework
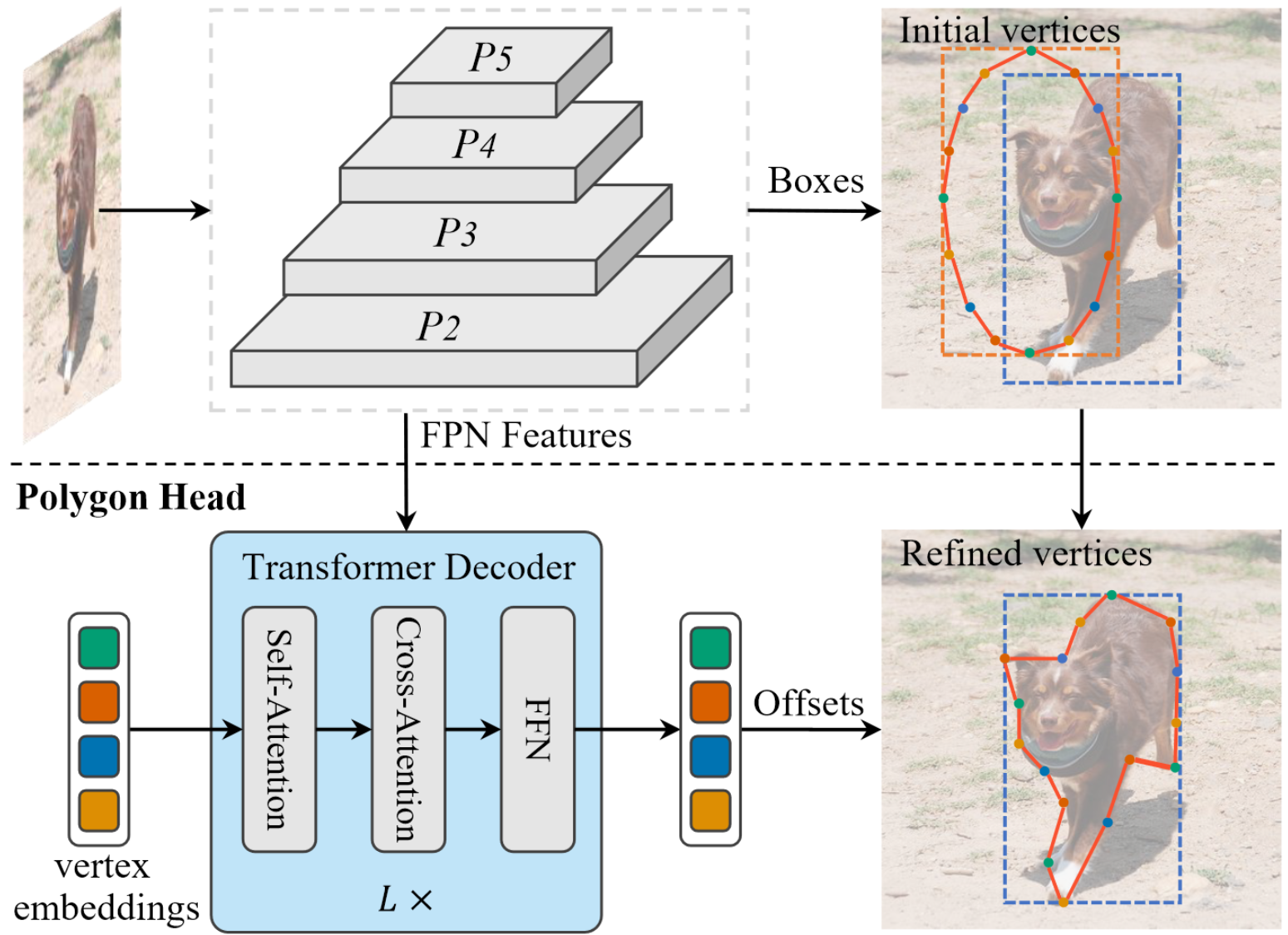
模型首先使用 ResNet 输出 box(此 box 采用 Mask R-CNN 的方式监督)和 FPN Features,并直接在全图按照椭圆采样初始化 polygon points
将 polygon points 进行 embedding 之后输入由一系列 SA 和 Cross-SA 组成的 transformer blocks,根据输出的 offset for each point 得到最终的输出
本文的工作重点不在于此框架,更应该关注的是如何使用损失函数约束 refined points。本文共提出了三个损失函数从三个不同的层面进行约束:
- Point-based Unary Loss:用于优化 refined points 的 box
这里的损失函数非常简单,使用 CIoU 进行 box-level 的监督。具体来说,i) 对最终输出的点集 $\mathcal{C}_r$,计算 $(x_1,y_1)=\min(\mathcal{C}_r),\ (x_2,y_2)=\max(\mathcal{C}_r)$,ii) 依据 $(x_1,y_1)$ 作为左上角,$(x_2,y_2)$ 作为右上角计算得到预测 box $b_c$,iii) 计算损失 $\mathcal{L}_u=1-CIoU(b_c,b_{gt})$。
在这样的损失监督下,即使是最好的情况,也只能保证 box-level 的预测,反映在多边形上可能是 random 的点或者在“更期望和原始 box 一致”的要求下尽可能像边缘移动,如下图 $(b)$ 所示。
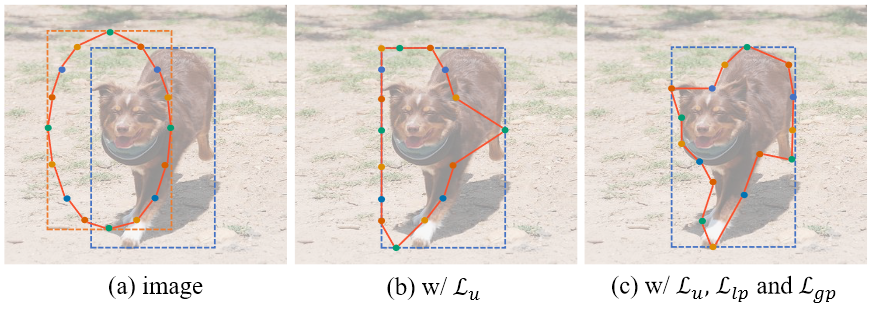
- Local Pairwise Loss:用于优化最终输出,使多边形边缘和像素变化位置重合
这是这篇文章最主要的贡献,讲道理想到“多边形边缘是像素变化较大的位置”并不困难,但如何设计对应的损失函数,既要反映此规律,又能正确回传梯度、有效率地优化不太容易。$\mathcal{L}_{lp}$ 大致可以描述为:在一个邻域内,任意两个像素之间的色彩相似度 $w$ 和分类惩罚 $\Delta u$(in box or not)乘积之和。简单来说,对于两个相近的色彩,色彩相似度 $w$ 会比较大,而如果此时两个像素没有被分到同一类,则 $\Delta u$ 也会很大,就会产生很大的惩罚项。模型会被迫让相似度大的像素被分为一类。
在位置 $(i,j)$ 处,记其 $k\times k$ 邻域内的像素集合为 $\Omega_k^{(i,j)}$,类别函数(一元)为 $\mathcal{U_C}$,相似度计算函数(二元)为 $\mathcal{W}$。定义相似度计算函数为:$\mathcal{W}(\mathcal{I}(i,j),\mathcal{I}(p,q))=\exp(-\frac{|\mathcal{I}(i,j)-\mathcal{I}(p,q)|_2}{2\tau_1^2})$,其中 $\tau_1$ 为温度超参。简单来说就是,颜色越像,值越大。
类别函数相对复杂:$\mathcal{U_C}(i,j)=\sigma(\frac{2\cdot(\Phi(i,j)-0.5)\cdot \mathcal{D_C}(i,j) }{\tau_2})$,其中 $\sigma$ 即为 Sigmoid;$\Phi(i,j)=1\ \mathrm{if}\ (i,j)\ \mathrm{in\ Polygon\ else\ 0}$ 表示点是否在多边形之中;$\mathcal{D_C}$ 是距离函数,表示 $(i,j)$ 距离最近的多边形边缘的欧氏距离;$\tau_2$ 是另一个温度超参。简单来说可以理解为 soft 的 0-1 分类函数。大致示意如下图:
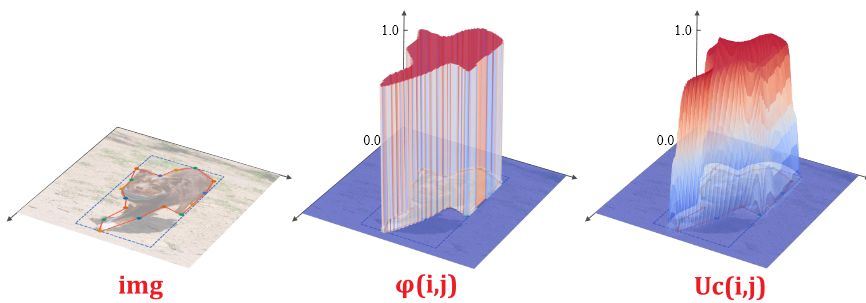
总结来说,约束相似颜色之间不存在多边形的损失函数为:
尽管 $\mathcal{U_C}$ 看上去很复杂,但其实际起到的作用就是硬分类函数 $\Phi$ 的作用,之所以搞复杂是因为 $\Phi$ 无法回传梯度,而 $\mathcal{U_C}$ 的梯度可以通过 $\mathcal{D_C}$ 回传到多边形点集上。
- Global Pairwise Loss:防止模型在 $\mathcal{L}_{lp}$ 优化下受到太多干扰(但实验似乎表明没有这种现象,同时 $\mathcal{L}_{gp}$ 的超参只有 0.03)
对于 $\mathcal{L}_{lp}$,模型可能受到大量的干扰(instance 内的像素变化位置太多,混淆了边界位置像素变化),因此 $\mathcal{L}_{gp}$ 用于清除这种混淆, $\mathcal{L}_{gp}$ 将会使 $\mathcal{U_C}$ 内/外的像素方差更小。由于 $\mathcal{U_C}$ 是 soft boundary,因此 $\mathcal{L}_{gp}$ 定义为:
其中 $u_{in},u_{out}$ 就表示 instance 内外的像素色彩均值,在 soft 的情况下定义为加权平均:
需要特别指出:上式中 $\Omega_c$ 指的并不是所有像素集合 $\Omega_{\mathcal I}$,而是按照预测的多边形点集 $\mathcal C$ 进行简单扩展并 crop&resize 得到的新图像,过程如下图所示。这很容易理解,因为 GP 的假设是 instance 内外的像素一致性,但是一张图有多个 instance,外部像素不可能一致,因此这种 clipped-image 当做的“global”才是更合理的。
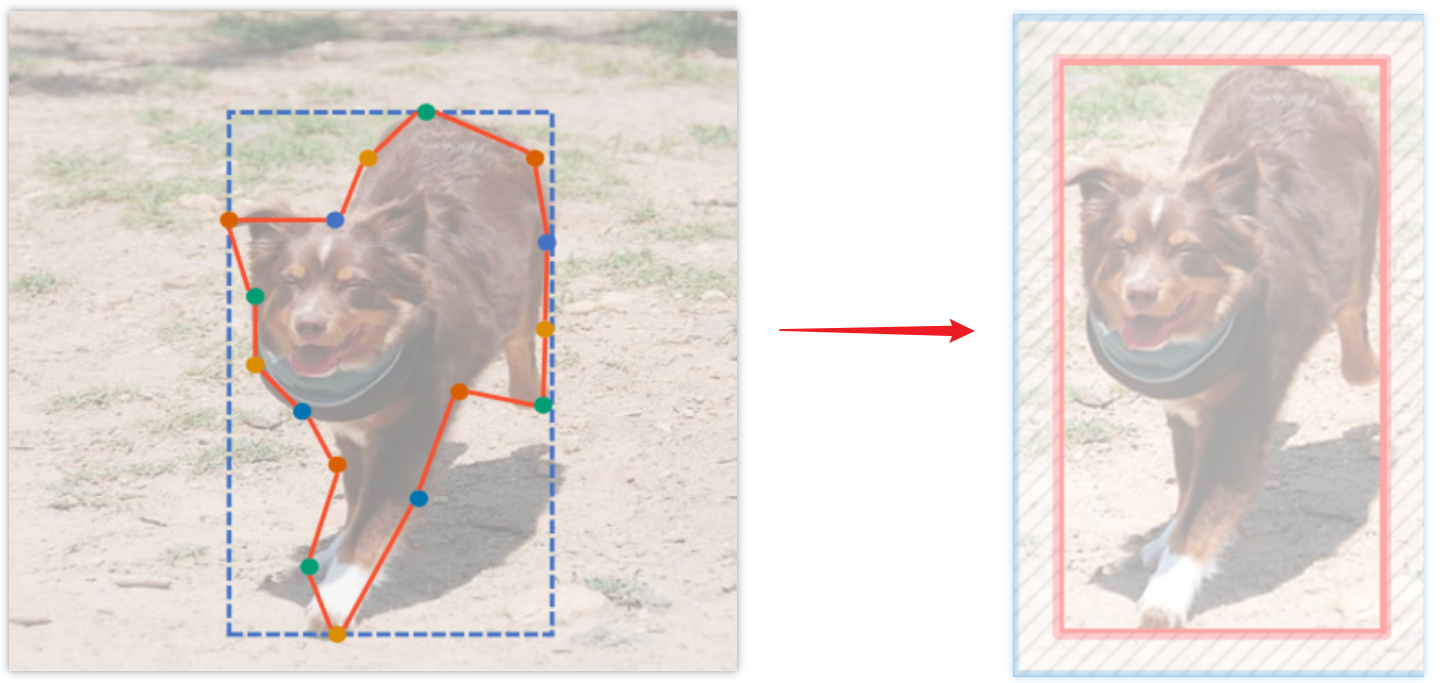
总结而言,三个损失函数直接按照线性进行组合:
experiment
大部分实验结果表明本方法有一定的提升能力,但也要注意到本方法是 box-2-polygon 的,和其他 box-2-mask 的方法本身就有着一定的优势。另外需要指出,在定量、定性的消融实验中,global pairwise 损失相对于 local pairwise 损失的有效性相当“轻微”